图神经网络的下游任务2-链路预测
图神经网络的下游任务2-链路预测
引言
前一篇博客介绍了如何利用图神经网络学习节点特征并进行节点分类任务。本文将介绍如何利用图神经网络进行链路预测这一下游任务。
看完以后应该可以回答以下几个问题:
- 链路预测是什么?
- 链路预测有什么应用?
- 如何利用图神经网络进行链路预测?
链路预测概述
本节引用部分主要摘自复杂网络链路预测的研究现状及展望。
链路预测定义
网络中的链路预测(Link Prediction)是指如何通过已知的网络节点以及网络结构等信息预测网络中尚未产生连边的两个节点之间产生链接的可能性。这种预测既包含了对未知链接(exist yet unknown links)的预测也包含了对未来链接(future links)的预测。

链路预测应用意义
链路预测在推荐系统、生化实验、数据分析等方面均有应用。
推荐系统
商品推荐:
在用户和商品的二部图中,如果用户购买商品,则用户和商品间存在链接,相似的用户可能同样会对该商品有需求,因此,预测用户和商品之间是否可能发生”购买“、”点击“等的链接,从而针对性地为用户推荐商品,可能可以提高商品的购买率。
好友推荐:
链路预测可以基于当前的网络结构去预测哪些现在尚未结交的用户“应该是朋友”,并将此结果作为“朋友推荐”发送给用户:如果预测足够准确,显然有助于提高相关网站在用户心目中的地位,从而提高用户对该网站的忠诚度。
生化实验
- 生物网络,例如蛋白质相互作用网络和新陈代谢网络,节点之间是否存在链接,或者说是否存在相互作用关系。事先在已知网络结构的基础上设计出足够精确的链路预测算法,再利用预测的结果指导试验,就有可能提高实验的成功率从而降低试验成本并加快揭开这类网络真实面目的步伐。
- 预测网络中的错误链接[14],这对于网络重组和结构功能优化有重要的应用价值。例如在很多构建生物网络的实验中存在暧昧不清甚至自相矛盾的数据[15],我们就有可能应用链路预测的方法对其进行纠正。
数据处理和分析
通过链路预测帮助补全数据缺失的网络。
分析演化网络,即对未来的预测。
在已知部分节点类型的网络(partially labeled networks)中预测未标签节点的类型——这可以用于判断一篇学术论文的类型[12]或者判断一个手机用户是否产生了切换运营商(例如从移动到联通)的念头[13]。
利用图神经网络进行链路预测
让我们再看下面这张图——基于消息传递网络框架搭建GNN流程。
与之前相对简单的任务不同,我们使用的数据集较大时,考虑分batch处理,此外,还补充了一些在构建数据集时可以做的操作,如数据增强、数据集划分、负采样等等。
这篇博客直接利用PyG内置数据集,重点关注红色框中的部分。
关于如何设计数据类可以参考另外一篇博客。
.jpg)
数据集介绍
PyG内置了大量常用的基准数据集,以PyG内置的Planetoid数据集为例。Planetoid数据集类的官方文档为torch_geometric.datasets.Planetoid。
我们在这里使用的是其中的Cora 数据,数据加载代码如下:
PS.若出现下载连接超时的情况可以参考《Planetoid无法直接下载Cora等数据集的3个解决方式》进行解决。
加载数据
from torch_geometric.datasets import Planetoid |
该数据包含 2708 篇科学出版物(节点),总共分为7类。引文网络由 5428 个引用链接(边)组成。数据集中的每个出版物都由一个 0/1 值的词向量描述,指示字典中相应词的缺失/存在。该词典由 1433 个独特的词组成,相对于一个one hot编码的词袋向量,此向量为节点的初始特征向量(data.x,shape为[2708,1433])。
其中,edge_index中存储了存在引文关系的节点信息,shape为[2,10556],同一列存储了两个存在引文关系的节点的索引(ID)。如代码打印结果中的:文献0引用了文献633,文献0引用了文献1862等。
数据集划分
我们利用PyG的工具函数train_test_split_edges(data,val_ratio=0.05, test_ratio=0.1)将数据划分成:训练集train、验证集validation(开发集development)、测试集test三个部分。该函数返回测试集和开发集的正/负链路样本索引列表,以及训练集的负链路mask矩阵。
from torch_geometric.utils import train_test_split_edges |
这里可能会有以下两个问题:
为什么要将数据集划分为三个部分?三个部分的作用?三个部分数据集的比例应如何设定?
另外一种常见的数据集划分方法是将数据集划分为两个部分(训练集和测试集),这种划分方法存在的问题在于,模型利用训练集数据进行训练,测试集数据进行模型泛化性测试。但我们不能利用测试集测试的bad case或者根据测试集的测试精度调整模型的参数。这是因为对于模型来说,数据集应该是只有训练集可见的,其他数据均不可见,如果利用测试集的结果调整模型相对于模型也”看到了“测试集的数据。将数据集划分为是独立同分布的三个部分就可以解决这个问题,将训练集数据用于模型训练,验证集(开发集)数据用于模型调参,测试集数据用于验证模型泛化性。
对于规模较小的数据集来说(10k及以下级别),训练集:验证集:测试集比例为6:2:2(划分两部分的话为7:3)较为合适,若数据集较大(如百万级),常见的比例为98:1:1 ,或者99.5:0.3:0.2等。
负链路样本是什么?为什么这里不直接返回训练集的负链路索引列表呢?继续往下读。
链路负采样
什么是负采样?为什么要负采样?
采集负样本,负样本与正样本相对,比如数据集中两个节点间存在链接,那么为一个正样本,两个节点间在已知数据集中不存在链接,那么构成一个负样本。
自然语言处理领域中,判断两个单词是不是一对上下文词(context)与目标词(target),如果是一对,则是正样本,如果不是一对,则是负样本。百度百科-负采样
根据数据集中的正样本,可以反向获取到大量的负样本,从中随机采集一部分负样本用于训练。
通常在图上存在边的节点对的数量往往少于不存在边的节点对的数量。为了类平衡,在每一个
epoch的训练过程中,我们只需要用到与正样本一样数量的负样本。综合以上两点原因,我们在每一个epoch的训练过程中都采样与正样本数量一样的负样本,这样我们既做到了类平衡,又增加了训练负样本的丰富性。链路预测中如何负采样?
在上一步中,我们利用train_test_split_edges()函数获取了测试集和验证集的正/负链路样本集合,存储在
data['val_pos_edge_index']、data['test_pos_edge_index']、data['val_neg_edge_index']、data['test_neg_edge_index']中。需要注意,利用该方法无法获取训练集的负样本,这是因为:在该函数中进行训练集的负样本采样相对于利用了测试集的正样本信息,而作为训练集我们应该只见训练集的信息,对验证集与测试集都是不可见的。所以,在训练过程中,我们需要利用
negative_sampling函数仅基于训练集进行负样本采样(也就是”第二次“负采样)。我们能获取到的数据集只是全域的一部分,三个数据集的负采样区域如下图所示:
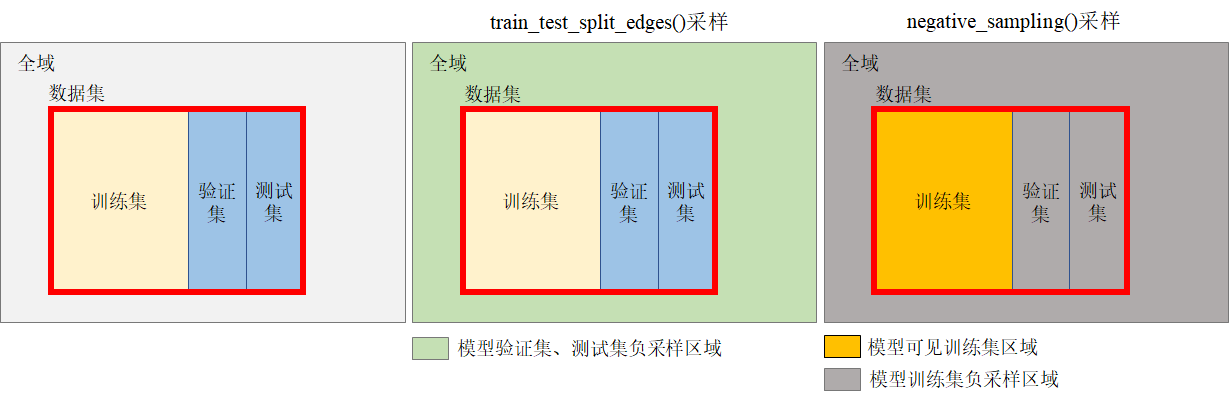
#负采样代码 |
实验
设计Net
用于做边预测的神经网络主要由两部分组成:其一是编码(encode),它与我们前面介绍的生成节点表征是一样的;其二是解码(decode),边两端节点的表征生成边为真的几率(odds)。
预测是将模型训练得到的两个节点特征计算存在连边的概率,比如:
节点0的特征为\(\mathbf x_0=[-0.0428, -0.0131, -0.0491, ..., 0.0481, -0.0185, 0.0379]\),
节点633的特征为\(\mathbf x_{633}=[-0.0394, -0.0124, -0.0441, ..., 0.0451, -0.0190, 0.0316],\)
则节点0和节点633连边存在的概率为:\(\mathbf x_0·\mathbf x_{633}^T=0.1450\)。
扩展到矩阵以加速运算,则计算公式为:\(\mathbf {Prob}=\mathbf X_0·\mathbf X_1^T\),其中\(X_0\)和\(X_1\)分别对应的是边两端的节点特征\(\mathbf X_0 =[\mathbf x_0,\mathbf x_1,....\mathbf x_n]^T\),\(\mathbf X_1=[\mathbf x_0,\mathbf x_1,....\mathbf x_n]^T\)。这可以算出\(\mathbf X_0\)中每个节点与\(\mathbf X_1\)中每个节点间链路存在的概率矩阵\(\mathbf {Prob}\)。
现在我们来写针对样本节点链路是否存在的decode函数和用于预测所有节点间链路是否存在的decode_all函数(二者本质计算方法相同)。
decode函数
在解码阶段,
pos_edge_index#[2,E1],neg_edge_index#[2,E2]是待预测的边,将二者拼接在一起进行预测edge_index[2,E1+E2]。edge_index[0]和edge_index[1]分别为边两端节点的索引,(z[edge_index[0]]*z[edge_index[1]]).sum(dim=-1)的计算示意如下图所示:
decode_all函数
decode_all(self, z)函数用于推断(inference)阶段,计算所有的节点间存在链路几率,z@z.t()的计算过程如下图所示。其中@符号表示矩阵乘法。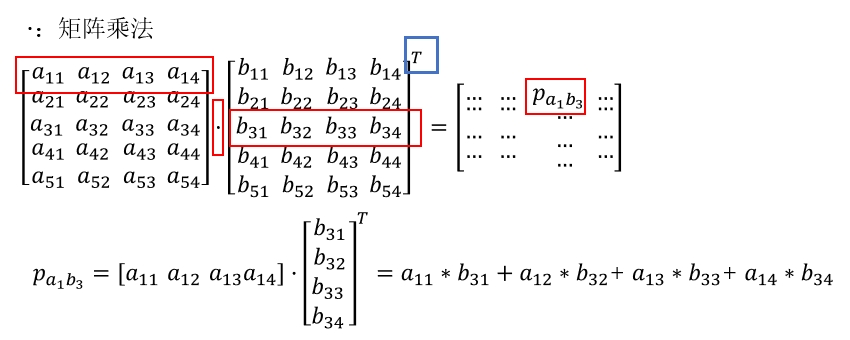
import torch |
选择优化器
如何选择优化器可以查看前一篇博客相关的总结:
#选择优化器 |
选择loss function
本文中的链路预测为预测有/没有链接,即二分类,可以选择二项交叉熵。(如何选择loss function可以查看前一篇博客相关的总结)
criterion = F.binary_cross_entropy_with_logits#注意这里不写括号 |
训练模型
def get_link_labels(pos_edge_index,neg_edge_index): |
PS.复习一下,下面这两段代码是相同的作用(消息传递图神经网络(Message Passing Neural Networks,MPNN) | 冬于的博客 (ifwind.github.io)):
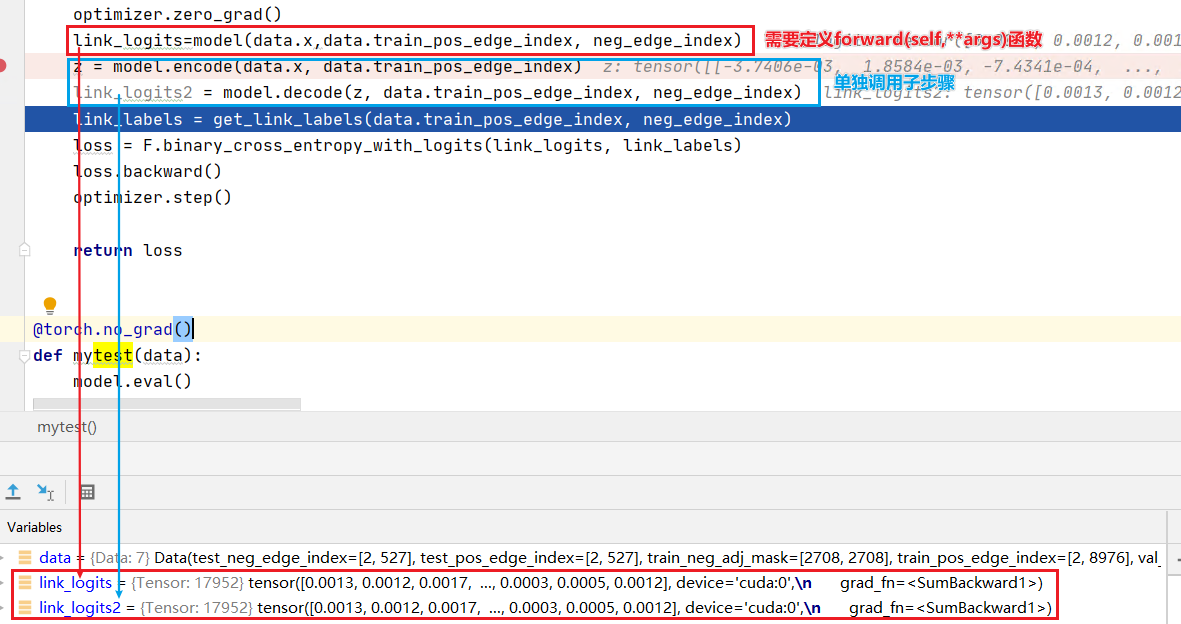
测试
利用测试集和验证集分别计算评价指标:
关于所选取的评价指标可以参考:roc_auc_score
为什么选择sigmoid而不是softmax计算概率?
sigmoid用于多分类任务(最终概率和可能超过1,一般来说某个类别的概率>0.5,就说明所属的类别包括该类别标签),而softmax用于分类任务(最终概率和为1,最大概率的类别为所属类别,一般只有1个)。我们这里要判断某个节点和其他多个节点是否存在链接,显然属于多分类任务(该节点可以和多个节点存在链接),因此选择sigmoid函数计算链路存在的概率。
from sklearn.metrics import roc_auc_score |
训练、验证和测试保存模型
best_val_auc = test_auc = 0 |
完整代码
总结几个小TIPS
为什么要将数据集划分为训练集、测试集、开发集三个部分?三个部分数据集的比例应如何设定?
将训练集数据用于模型训练,验证集(开发集)数据用于模型调参,测试集数据用于验证模型泛化性。这样测试集数据相对于模型完全不可见,可以比较准确地检验模型的有效性。
对于规模较小的数据集来说(10k及以下级别),训练集:验证集:测试集比例为6:2:2(划分两部分的话为7:3)较为合适,若数据集较大(如百万级),常见的比例为98:1:1 ,或者99.5:0.3:0.2等。
为什么训练集要”第二次“负采样?
为了保证模型只可见训练集信息,负采样也要在只基于训练集正样本信息的基础上采样。
以data.train_pos_edge_index为实际参数来进行训练集负样本采样,但这样采样得到的负样本可能包含一些验证集的正样本与测试集的正样本,即可能将真实的正样本标记为负样本,由此会产生冲突。但我们还是这么做,这是为什么?
因为要保证验证集和测试集的信息不可见。
为什么选择sigmoid而不是softmax计算概率?
sigmoid用于多分类任务(最终概率和可能超过1,一般来说某个类别的概率>0.5,就说明所属的类别包括该类别标签),而softmax用于分类任务(最终概率和为1,最大概率的类别为所属类别,一般只有1个)。判断某个节点和其他多个节点是否存在链接,显然属于多分类任务(该节点可以和多个节点存在链接),因此选择sigmoid函数计算链路存在的概率。