Cluster-GCN：超大图上的节点特征学习

引言

基于图卷积设计的图神经网络在非结构化数据上表现优良，但仍然面临一些困难，如：

在超大图上进行图神经网络的训练时，全图的图卷积操作和full-batch的梯度下降方式，每个epoch中同时对所有节点更新embedding需要大量的内存空间（空间复杂度高）；
基于图卷积操作的图神经网络结构，随着层数增加，计算成本指数增加（时间复杂度高），过多层的图神经网络模型还存在输出节点特征过平滑的特点；
full-batch算法收敛性较差。

现有应对方案

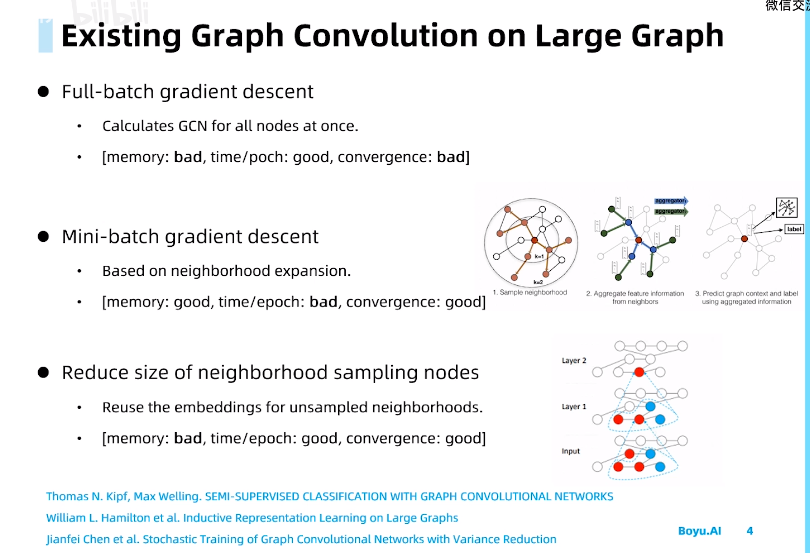
针对空间复杂度高的问题，有学者提出基于mini-batch的梯度下降方式减小模型的内存需求。

如GraphSAGE模型，该方法对节点周围k步的邻居进行采样，由于采样的邻居数小于full-batch，空间复杂度较小；然而由于需要更新节点embedding需要考虑邻居节点，随着GCN层数提升，计算量指数级增加，时间复杂度高。但该方法可以选取合适的batchsize，收敛性相对full-batch好一些；
而针对mini-batch中时间复杂度高的问题，有学者提出VR-GCN模型，该模型保存之前sample时计算过的节点的embedding，可以降低时间复杂度，但需要存储sample过的节点的embedding，空间复杂度又相对变得很高。

Cluster-GCN

针对以上方案解决图神经网面对困难的不足，论文Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Network提出了一种新的图神经网络的训练方法。其目标在于：优化图卷积网络的计算方式，能在大型图上训练更深的GCN，并能比较好收敛，提升性能（较低的时间、空间复杂度+较好的收敛）。

根据对问题的分析和现有方案解决问题存在的不足，逐步分析问题并提出相应的解决思路。

为什么mini-batch的方法时间复杂度高？

基于mini-batch的方法在参数更新中，不需要计算完整梯度，只需要计算每个batch的梯度。使用\(\mathcal{B} \subseteq[N]\)来表示一个batch，其大小为\(b=|\mathcal{B}|\)。SGD的每一步都将计算梯度估计值\(\frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \nabla \operatorname{loss}\left(y_{i}, z_{i}^{(L)}\right)\)来进行参数更新。尽管在epoches数量相同的情况下，采用SGD方式进行训练，收敛速度可以更快，但此种训练方式会每个epoch引入额外的时间开销。

将节点\(i\)的梯度的计算表示为\(\nabla \operatorname{loss}\left(y_{i}, z_{i}^{(L)}\right)\)，它依赖于节点\(i\)的\(L\)层的表征，而节点\(i\)的非第\(0\)层的表征都依赖于各自邻接节点在前一层的表征（邻域扩展）。假设一个图神经网络有\(L+1\)层，节点的平均的度为\(d\)。为了得到节点\(i\)的梯度，均我需要聚合图上\(O\left(d^{L}\right)\)的节点的表征。也就是说，我们需要获取节点的距离为\(k(k=1, \cdots, L)\)的邻接节点的信息来进行一次参数更新。由于要与权重矩阵\(W^{(l)}\)相乘，所以计算任意节点表征的时间开销是\(O\left(F^{2}\right)\)。所以平均来说，一个节点的梯度的计算需要\(O\left(d^{L} F^{2}\right)\)的时间。

为了反映mini-batch SGD的计算效率，Cluster-GCN论文提出了"表征利用率"的概念来描述计算效率。在训练过程中，如果节点\(i\)在\(l\)层的表征\(z_{i}^{(l)}\)被计算并在\(l+1\)层的表征计算中被重复使用\(u\)次，那么\(z_{i}^{(l)}\)的表征利用率为\(u\)。一个batch有多个节点，不同的节点同样距离远的邻接节点可以是重叠的，于是计算表征的次数可以小于最坏的情况\(O\left(b d^{L}\right)\)。对于随机抽样的mini-batch SGD，\(u\)非常小，因为图通常是大且稀疏的。假设\(u\)是一个小常数（节点间同样距离的邻接节点重叠率小），那么mini-batch SGD的训练方式对每个batch需要计算\(O\left(b d^{L}\right)\)的表征，于是每次参数更新需要\(O\left(b d^{L} F^{2}\right)\)的时间，每个epoch需要\(O\left(N d^{L} F^{2}\right)\)的时间。

基于full-batch梯度下降的方法具有最大的表征利用率（时间复杂度较低）——每个节点表征将在上一层被重复使用平均节点度次。因此，全梯度下降法在每个epoch中只需要计算\(O(N L)\)的表征，这意味着平均下来只需要\(O(L)\)的表征计算就可以获得一个节点的梯度。

因此，解决的问题转化为：

能否找到一种将节点分成多个batch的方式，对应地将图划分成多个子图，使得表征利用率最大？

为了最大限度地提高表征利用率，理想的划分batch的结果是，batch内的边尽可能多，batch之间的边尽可能少。

由此引入图聚类算法提出解决策略1：

解决策略1——每个聚类簇作为一个batch

其基本思路为：

利用图节点聚类算法将一个图的节点划分为\(c\)个簇，每一次选择几个簇的节点和这些节点对应的边构成一个子图，然后对子图做训练。
由于是利用图节点聚类算法将节点划分为多个簇，所以簇内边的数量要比簇间边的数量多得多，所以可以提高表征利用率，并提高图神经网络的训练效率。

对于一个图\(G\)，我们将其节点划分为\(c\)个簇：\(\mathcal{V}=\left[\mathcal{V}_{1}, \cdots \mathcal{V}_{c}\right]\)，其中\(\mathcal{V}_{t}\)由第\(t\)个簇中的节点组成，对应的我们有\(c\)个子图： \[ \bar{G}=\left[G_{1}, \cdots, G_{c}\right]=\left[\left\{\mathcal{V}_{1}, \mathcal{E}_{1}\right\}, \cdots,\left\{\mathcal{V}_{c}, \mathcal{E}_{c}\right\}\right] \notag \] 其中\(\mathcal{E}_{t}\)只由\(\mathcal{V}_{t}\)中的节点之间的边组成。经过节点重组，邻接矩阵被划分为大小为\(c^{2}\)的块矩阵，如下所示 \[ A=\bar{A}+\Delta=\left[\begin{array}{ccc} A_{11} & \cdots & A_{1 c} \\ \vdots & \ddots & \vdots \\ A_{c 1} & \cdots & A_{c c} \end{array}\right] \tag{1} \] 其中， \[ \bar{A}=\left[\begin{array}{ccc} A_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & A_{c c} \end{array}\right], \Delta=\left[\begin{array}{ccc} 0 & \cdots & A_{1 c} \\ \vdots & \ddots & \vdots \\ A_{c 1} & \cdots & 0 \end{array}\right] \tag{2} \] 其中，对角线上的块\(A_{t t}\)是大小为\(\left|\mathcal{V}_{t}\right| \times\left|\mathcal{V}_{t}\right|\)的邻接矩阵，它由\(G_{t}\)内部的边构成。\(\bar{A}\)是图\(\bar{G}\)的邻接矩阵。\(A_{s t}\)由两个簇\(\mathcal{V}_{s}\)和\(\mathcal{V}_{t}\)之间的边构成。\(\Delta\)是由\(A\)的所有非对角线块组成的矩阵。同样，我们可以根据\(\left[\mathcal{V}_{1}, \cdots, \mathcal{V}_{c}\right]\)划分节点表征矩阵\(X\)和类别向量\(Y\)，得到\(\left[X_{1}, \cdots, X_{c}\right]\)和\(\left[Y_{1}, \cdots, Y_{c}\right]\)，其中\(X_{t}\)和\(Y_{t}\)分别由\(V_{t}\)中节点的表征和类别组成。

用块对角线邻接矩阵\(\bar{A}\)去近似邻接矩阵\(A\)，这样做的好处是，完整的损失函数（公示(2）)可以根据batch分解成多个部分之和。

以\(\bar{A}^{\prime}\)表示归一化后的\(\bar{A}\)，单层卷积过程： \[ X^{(l+1)}=\sigma\left(A^{\prime} X^{(l)} W^{(l)}\right)\tag{3} \] 经过多层卷积后，最后一层节点表征矩阵可以做如下的分解： \[ \begin{aligned} Z^{(L)} &=\bar{A}^{\prime} \sigma\left(\bar{A}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}^{\prime} X W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)} \\ &=\left[\begin{array}{c} \bar{A}_{11}^{\prime} \sigma\left(\bar{A}_{11}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}_{11}^{\prime} X_{1} W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)} \\ \vdots \\ \bar{A}_{c c}^{\prime} \sigma\left(\bar{A}_{c c}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}_{c c}^{\prime} X_{c} W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)} \end{array}\right] \end{aligned} \tag{4} \] 由于\(\bar{A}\)是块对角形式（\(\bar{A}_{t t}^{\prime}\)是\(\bar{A}^{\prime}\)的对角线上的块），于是损失函数可以分解为 \[ \begin{aligned}\mathcal{L}_{\bar{A}^{\prime}}=\sum_{t} \frac{\left|\mathcal{V}_{t}\right|}{N} \mathcal{L}_{\bar{A}_{tt}^{\prime}} \text {and} \mathcal{L}_{\bar{A}_{tt}^{\prime}}=\frac{1}{\left|\mathcal{V}_{t}\right|} \sum_{i \in \mathcal{V}_{t}} \operatorname{loss}\left(y_{i}, z_{i}^{(L)}\right)\end{aligned} \tag{5} \]

基于公式(4)和公式(5)，在训练的每一步中，Cluster-GCN首先采样一个簇\(\mathcal{V}_{t}\)，然后根据\(\mathcal{L}_{\bar{A}_{tt}^{\prime}}\) 的梯度进行参数更新。这种训练方式，只需要用到子图\(A_{t t}\), \(X_{t}\), \(Y_{t}\)以及神经网络权重矩阵\(\{W^{(l)}\}_{l=1}^{L}\)。实际中，主要的计算开销在神经网络前向过程中的矩阵乘法运算（公式(4)的一个行）和梯度反向传播。

论文利用图聚类算法构建batch的方法和随机采样节点构建batch的方法进行对比，结果表明聚类分区得到更好的性能（就测试F1集得分而言）。

Dataset	random partition	clustering partition
Cora	78.4	82.5
Pubmed	78.9	79.9
PPI	68.1	92.9

解决策略1（将聚类簇作为batch）还存在什么问题？

上述利用图聚类算法构建batch的策略还存在以下两个问题：

图被分割后，一些边（公式(2)中的\(\Delta\)部分）被移除，即，丢失了聚类簇之间的连边信息，性能可能因此会受到影响。
图聚类算法倾向于将相似的节点聚集在一起。因此，单个簇中节点的类别分布可能与原始数据集不同，且不同batch的分布差别很大，导致对梯度的估计有偏差。

图2展示了一个类别分布不平衡的例子，该例子使用Reddit数据集，节点聚类由Metis软件包实现。根据各个簇的类别分布来计算熵值。与随机划分相比，采用聚类划分得到的大多数簇熵值都很小，簇熵值小表明簇中节点的标签分布偏向于某一些类别，这意味着不同簇的标签分布有较大的差异，这将影响训练的收敛。

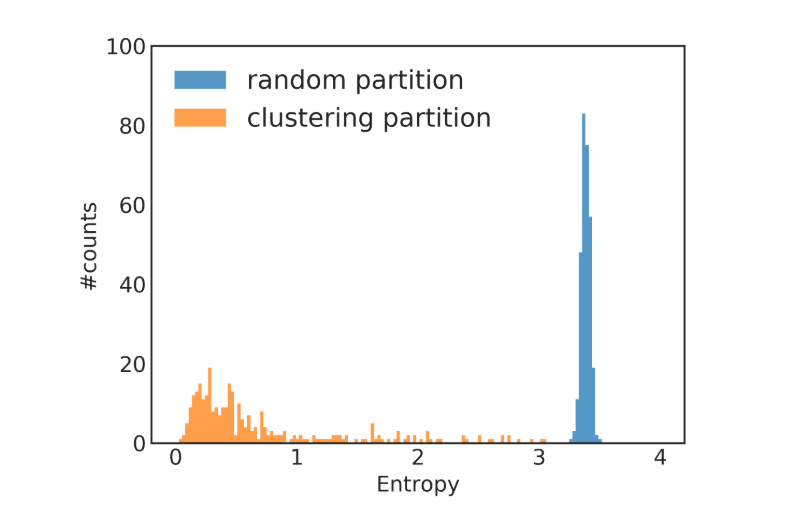
[^]: 图2：类别分布熵值柱状图。类别分布熵越高意味着簇内类别分布越平衡，反之意味着簇内类别分布越不平衡。此图展示了不同熵值的随机分区和聚类分区的簇的数量，大多数聚类分区的簇具有较低的熵，表明各个簇内节点的类别分布存在偏差。相比之下，随机分区会产生类别分布熵很高的簇，尽管基于随机分区的训练的效率较低。在这个例子中，使用了Reddit数据集，进行了300个簇的分区。

解决策略2——随机分区聚类簇作为batch

为了解决上面两个问题，进一步使用分区的概念，提出一种随机多聚类方法，随机选择多个簇作为一个分区，以分区为单位作为一个batch，减少batch间的差异（variance）。

此方法首先将图划分为\(p\)个簇，\(\mathcal{V}_{1}, \cdots, \mathcal{V}_{p}\)，\(p\)是一个较大的值，在构建一个batch时，不是只使用一个簇，而是使用随机选择的\(q\)个簇合并到一个区，表示为\(t_{1}, \ldots, t_{q}\)，恢复区内各个cluster间的连边，以分区作为batch，其中包含节点\(\left\{\mathcal{V}_{t_{1}} \cup \cdots \cup \mathcal{V}_{t_{q}}\right\}\) 、簇内边\(\left\{A_{i i} \mid i \in t_{1}, \ldots, t_{q}\right\}\)和簇间边\(\left\{A_{i j} \mid i, j \in t_{1}, \ldots, t_{q}\right\}\)。此方法的好处有，1）不会丢失簇间的边，2）不会有很大的batch内类别分布的偏差，3）以及不同的epoch使用的batch不同，这可以降低梯度估计的偏差，4）基于小图进行训练，不会消耗很多内存空间，且于是可以尝试训练更深的神经网络。

图3展示了随机多簇方法，在每个epoch中，随机选择一些簇来组成一个batch，不同的epoch的batch不同。在图4中，可以观察到，使用多个簇来组成一个batch可以提高收敛性。最终的Cluster-GCN算法在算法1中呈现。

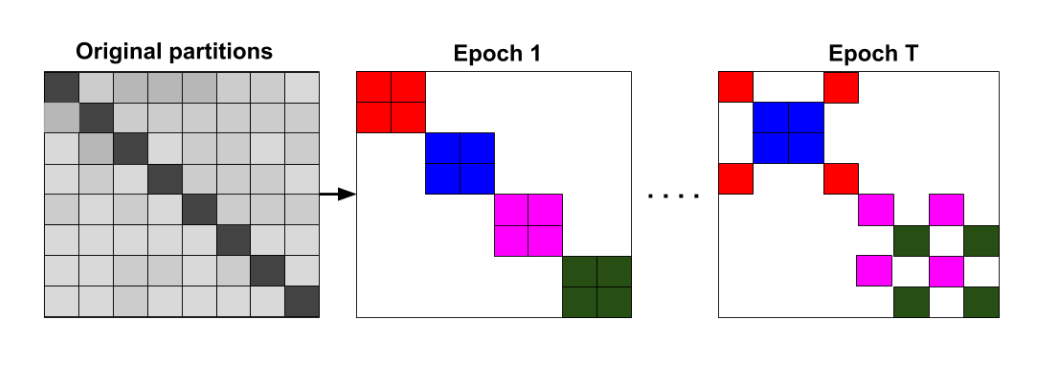
[^]: 图3：Cluster-GCN提出的随机多分区方法。在每个epoch中，我们（不放回地）随机抽取\(q\)个簇（本例中使用\(q\)=2）及其簇间的边，来构成一个batch（相同颜色的块在同一batch中）。

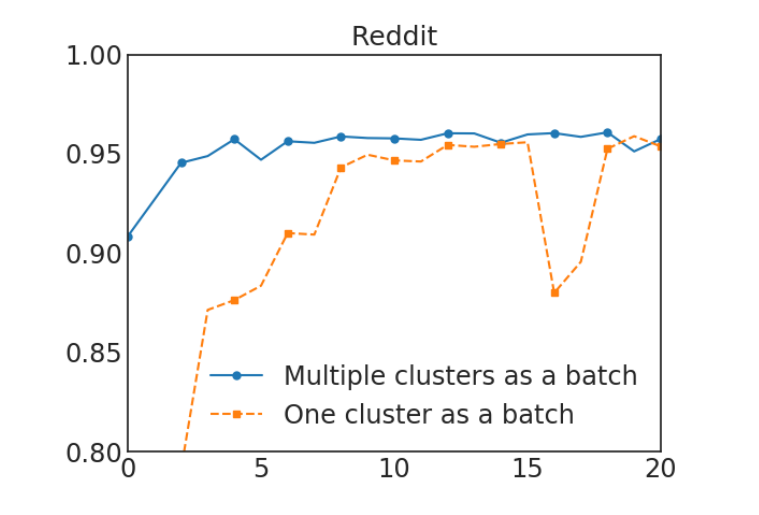
[^]: 图4：选择一个簇与选择多个簇的比较。前者使用300个簇。后者使用1500个簇，并随机选择5个簇来组成一个batch。该图X轴为epoches，Y轴为F1得分。

如何解决深层GCNs的问题？

与其他神经网络增加卷积层数可能会带来比较大的效果提升不同，以往尝试训练更深的GCN的研究似乎表明，增加更多的层是没有帮助的。比如由于节点数量过少，过深的层很容易出现过拟合的问题。此外，加深GCN神经网络层数后，训练变得很困难，因为层数多了之后前面的信息可能无法传到后面。有的研究采用了一种类似于残差连接的技术，使模型能够将前一层的信息直接传到下一层。具体来说，他们修改了公式(3)，将第\(l\)层的表征添加到下一层，如下所示： \[ X^{(l+1)}=\sigma\left(A^{\prime} X^{(l)} W^{(l)}\right)+X^{(l)} \tag{6} \]

解决策略——对角增强+标准化

Cluster-GCN论文中提出了另一种简单的技术来改善深层GCN神经网络的训练。在原始的GCN的设置里，每个节点都聚合邻接节点在上一层的表征。Cluster-GCN考虑层的距离，即近距离的邻接节点应该比远距离的的邻接节点贡献更大。其主要思想是放大GCN每一层中使用的邻接矩阵\(A\)的对角线部分。通过这种方式，在GCN的每一层的聚合中对来自上一层的表征赋予更大的权重。这可以通过给\(\bar{A}\)加上一个单位矩阵\(I\)来实现，如下所示， \[ X^{(l+1)}=\sigma\left(\left(A^{\prime}+I\right) X^{(l)} W^{(l)}\right) \tag{7} \] 虽然公式(9)似乎是合理的，但对所有节点使用相同的权重而不考虑其邻居的数量可能不合适。此外，它可能会受到数值不稳定的影响，因为当使用更多的层时，数值会呈指数级增长。因此，Cluster-GCN方法提出了一个修改版的公式(9)，以更好地保持邻接节点信息和数值范围。首先给原始的\(A\)添加一个单位矩阵\(I\)，并进行归一化处理 \[ \tilde{A}=(D+I)^{-1}(A+I) \tag{8} \] 然后考虑， \[ X^{(l+1)}=\sigma\left((\tilde{A}+\lambda \operatorname{diag}(\tilde{A})) X^{(l)} W^{(l)}\right) \tag{9} \]

其中，\(\lambda\)为超参数。

结果如下：

源码分析

原文中利用了四个数据集（PPI、Reddit、Reddit2、Amazon），我们这里利用较小的Reddit2来进行实验。

数据加载

该数据集包含41个分类任务，232,965个节点，23,213,838条边，节点维度为602维。

from torch_geometric.datasets import Reddit
from torch_geometric.data import ClusterData, ClusterLoader, NeighborSampler

dataset = Reddit('data/Reddit2')
data = dataset[0]
print(dataset.num_classes)
print(data.num_nodes)
print(data.num_edges)
print(data.num_features)
#41
#232965
#23213838
#602

图节点聚类与数据加载器生成

cluster_data = ClusterData(data, num_parts=1500, recursive=False, save_dir=dataset.processed_dir)
train_loader = ClusterLoader(cluster_data, batch_size=20, shuffle=True, num_workers=12)
subgraph_loader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=1024, shuffle=False, num_workers=12)

cluster_data遵循Cluster-GCN提出的方法，图节点被聚类划分成多个簇并组成多个分区。ClusterData继承于Dataset类，num_parts对应论文中的分区个数；

train_loader为数据加载器返回的一个batch由多个簇组成。ClusterLoader继承于DataLoader类，num_worker表示线程数。

subgraph_loader用于全图的推理阶段，不对图节点聚类，使用所有可用边逐层计算节点特征可以加速计算，而不是立即计算每批的最终表示。

设计Net

卷积层优化——for deeper GCNs

在forward()中，实现对角增强+标准化策略以便可以训练更深层次的GCN网络。

#卷积层优化
class GCNConv(MessagePassing):
    _cached_edge_index: Optional[Tuple[Tensor, Tensor]]
    _cached_adj_t: Optional[SparseTensor]

    def __init__(self, in_channels: int, out_channels: int,
                 improved: bool = False, cached: bool = False,
                 add_self_loops: bool = True, normalize: bool = True,
                 bias: bool = True,lamb: float=1, **kwargs):

        kwargs.setdefault('aggr', 'add')
        super(GCNConv, self).__init__(**kwargs)

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.improved = improved
        self.cached = cached
        self.add_self_loops = add_self_loops
        self.normalize = normalize

        self._cached_edge_index = None
        self._cached_adj_t = None

        self.weight = Parameter(torch.Tensor(in_channels, out_channels))

        self.lamb=lamb
        if bias:
            self.bias = Parameter(torch.Tensor(out_channels))
        else:
            self.register_parameter('bias', None)

        self.reset_parameters()

    def reset_parameters(self):
        glorot(self.weight)
        zeros(self.bias)
        self._cached_edge_index = None
        self._cached_adj_t = None

    def forward(self, x: Tensor, edge_index: Adj,
                edge_weight: OptTensor = None) -> Tensor:
        adjmat,_ = add_self_loops(edge_index=edge_index,edge_weight=edge_weight)#A+I
        row, col = adjmat
        adjmat = SparseTensor(row=adjmat[0], col=adjmat[1], value=torch.ones(adjmat.shape[1]))
        deg_norm = degree(col, adjmat.size(0), dtype=torch.long).pow(-1) #计算D
        A_hat=adjmat.to_dense()
        #计算1、\tilde{A}=(D+I)^{-1}(A+I) 公式(8)
        #计算2、\tilde{A}+\lambda \operatorname{diag}(\tilde{A})
        A_hat=deg_norm*(A_hat)+self.lamb*torch.diag(A_hat)*torch.eye(A_hat.shape[0])
        A_hat=SparseTensor.from_dense(A_hat)

        x = x @ self.weight

        # propagate_type: (x: Tensor, edge_weight: OptTensor)
        out = self.propagate(A_hat, x=x)
        if self.bias is not None:
            out += self.bias
        return out

    def message_and_aggregate(self, A_hat: SparseTensor, x: Tensor) -> Tensor:
        #计算3、(\tilde{A}+\lambda \operatorname{diag}(\tilde{A})) X^{(l)} W^{(l)}
        return matmul(A_hat, x, reduce=self.aggr)

    def __repr__(self):
        return '{}({}, {})'.format(self.__class__.__name__, self.in_channels,
                                   self.out_channels)

网络结构

class Net(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.convs = ModuleList(
            [GCNConv(in_channels, 128),
             GCNConv(128, out_channels)])

    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i != len(self.convs) - 1:
                x = F.relu(x) #计算4、\sigma\left((\tilde{A}+\lambda \operatorname{diag}(\tilde{A})) X^{(l)} W^{(l)}\right)
                x = F.dropout(x, p=0.5, training=self.training)
        return F.log_softmax(x, dim=-1)

    def inference(self, x_all):
        pbar = tqdm(total=x_all.size(0) * len(self.convs))
        pbar.set_description('Evaluating')

        # Compute representations of nodes layer by layer, using *all*
        # available edges. This leads to faster computation in contrast to
        # immediately computing the final representations of each batch.
        for i, conv in enumerate(self.convs):
            xs = []
            for batch_size, n_id, adj in subgraph_loader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)
                x_target = x[:size[1]]
                x = conv((x, x_target), edge_index)
                if i != len(self.convs) - 1:
                    x = F.relu(x)
                xs.append(x.cpu())
                pbar.update(batch_size)
            x_all = torch.cat(xs, dim=0)

        pbar.close()
        return x_all

可以看到此神经网络拥有forward和inference两个方法。forward函数的定义与普通的图神经网络并无区别。inference方法应用于推理阶段，为了更快计算，所以使用subgraph_loader。

这里利用nn.ModuleList存储不同的模块，需要注意的是：

nn.ModuleList 并没有定义一个网络，它只是将不同的模块储存在一起，这个 ModuleList 里面的顺序并不能决定什么，网络的执行顺序是根据 forward 函数来决定的。

这不同于 nn.Sequential，里面的模块是按照顺序进行排列的，必须确保前一个模块的输出大小和下一个模块的输入大小是一致的。摘自：PyTorch 中的 ModuleList 和 Sequential: 区别和使用场景

补充：

Tqdm 是一个快速，可扩展的Python进度条，可以在 Python 长循环中添加一个进度提示信息，用户只需要封装任意的迭代器 tqdm(iterator)。摘自：tqdm介绍及常用方法_GZKPeng的博客-CSDN博客_tqdm

100%|███████████████████████████████████| 857K/857K [00:04<00:00, 246Kloc/s]

训练、验证与测试

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

def train():
    model.train()

    total_loss = total_nodes = 0
    for batch in train_loader:
        batch = batch.to(device)
        optimizer.zero_grad()
        out = model(batch.x, batch.edge_index)
        loss = F.nll_loss(out[batch.train_mask], batch.y[batch.train_mask])
        loss.backward()
        optimizer.step()

        nodes = batch.train_mask.sum().item()
        total_loss += loss.item() * nodes
        total_nodes += nodes

    return total_loss / total_nodes

@torch.no_grad()
def test():  # Inference should be performed on the full graph.
    model.eval()

    out = model.inference(data.x)
    y_pred = out.argmax(dim=-1)

    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = y_pred[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs


for epoch in range(1, 31):
    loss = train()
    if epoch % 5 == 0:
        train_acc, val_acc, test_acc = test()
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, '
              f'Val: {val_acc:.4f}, test: {test_acc:.4f}')
    else:
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}')