GIN：逼近WL-test的GNN架构

引言

之前提到了如何设计图神经网络进行节点表征学习，并基于此开展下游任务1节点分类和下游任务2链路预测。

本篇博文将关注利用GNN进行图级别表示的学习。图表征学习要求根据节点属性、边和边的属性（如果有的话）生成一个向量作为图的表征，基于图表征可以做图的预测。基于图同构网络（Graph Isomorphism Network, GIN）的图表征网络是当前最经典的图表征学习网络。

本文将以GIN为例，首先将介绍图同构的相关概念，然后介绍图同构测试的经典算法——Weisfeiler-Lehamn算法，接着解释为什么说GNN是WL-test的变体，并分析基于消息传递网络架构设计的GNN模型如何学习图表征，而现有的GNN模型如GCN等为什么达不到WL-test，最后介绍How Powerful are Graph Neural Networks?一文中作者提出的GIN架构，并提供相应模块的代码。

看完以后应该可以回答以下几个问题：

  1. 什么是同构图？
  2. 为什么要计算图同构？
  3. 什么是WL-test？
  4. GNN与WL-test的相似之处？
  5. 为什么要用GNN代替WL-test算法？
  6. 如何用GNN学习图表示（特征）？
  7. 现有的GNN模型，如GCN、GraphSAGE相对差在哪里？（为什么GCN、GraphSAGE无法区分简单的图结构？）
  8. GIN的架构？

图同构Graph Isomorphism

参考【离散数学】图论（七）图的同构中给出的定义：

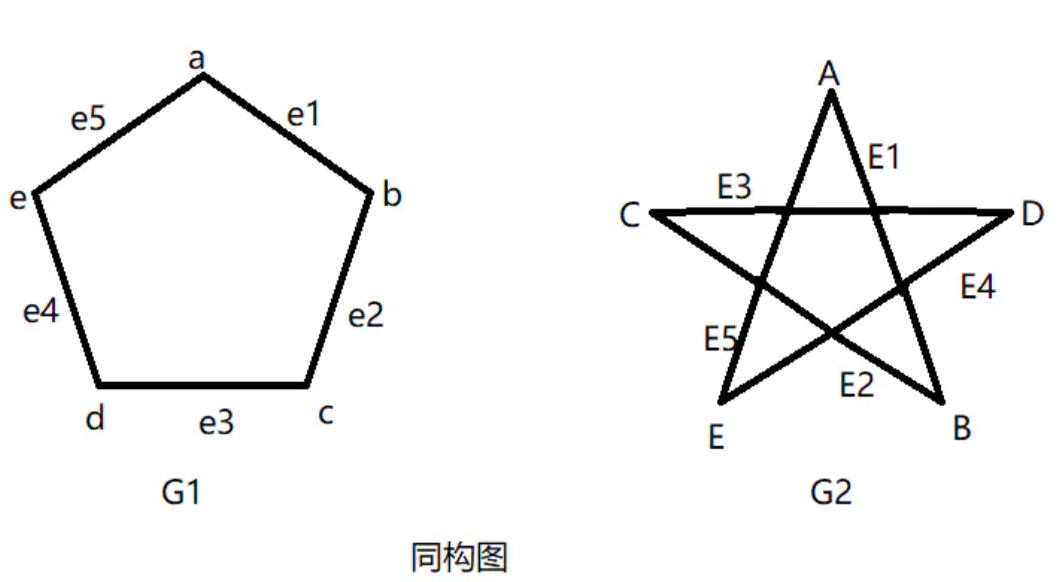
上图中，G1和G2为同构的，因为：

  1. 从G1的结点到G2的结点，存在一个一对一的映上函数 \(f\) (one - to - one and onto function \(f\) )
  2. 从G1的边到G2的边，存在一个一对一的映上函数 \(g\) (one - to - one and onto function \(g\) )
  • G1中，边e1与结点a，b相关联，当且仅当(if and only if) G2中边 g(e) 与结点 f(a) 和 f(b) 相关联（E1和结点A，B相关联）。若满足此条件，函数 f 和 g 称为从G1到G2的同构映射(Isomorphism)

简单来说，两个图中的节点和边数量相同且边的连接关系相同，则两个图同构，两个图在拓扑上等价。

图同构测试的意义

比如在蛋白质结构、基因网络中，具有相似结构（同构测试或相似度计算）的蛋白质或基因结构可能具有相似的功能特性。又比如两位作者相似的期刊引文网络结构可能表示两位作者的研究内容相似等等。

WL-test(Weisfeiler-Lehamn test)

图同构问题通常被认为是 NP 问题，Weisfeiler-Lehman算法(威斯费勒-莱曼算法)是测试图同构的经典算法之一Weisfeiler-Lehman Graph Kernels。但是Weisfeiler-Lehman 测试（WL-test）是图同构的一个必要但不充分的条件。也就是说，两个图的WL-test结果显示有差异，可认为这两个图是非同构的；但如WL-test结果显示没有差异，只能表述为这两个图可能同构。

WL 算法可以是 K-维的，K-维 WL 算法在计算图同构问题时会考虑顶点的 k 元组，如果只考虑顶点的自身特征（如标签、颜色等），那么就是 1-维 WL 算法。

接下来我们举两个例子介绍1维WL-test的计算步骤。

WL-test计算步骤

WL-test包括四个步骤：聚合邻居节点标签；多重集排序；标签压缩；更新标签。

多重集（Multiset）：一组可能重复的元素集合。例如：{1,1,2,3}就是一个多重集合。

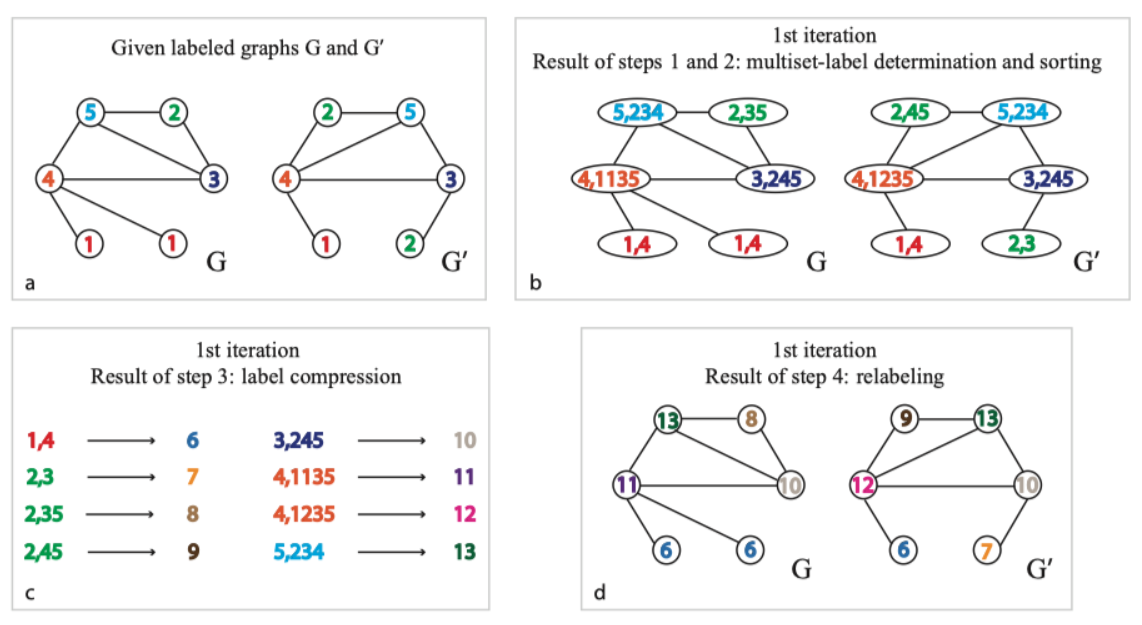
下图a首先给出了两个标签标记（如果没有节点标签，可以用节点的度作为标签）的图 \(G\),\(G'\)。（这个例子中两个图显然是不同构的，因为图\(G\)中有两个标签为1的节点而图\(G'\)中只有一个标签为1的节点）

  1. 聚合邻居节点标签(图b)

    在第一步中，考虑各个节点的1阶邻居节点，构建集合（如图\(G\)中的节点5，其周围节点为4、3、2，则经过步骤1生成的多重集为(5,4-3-2)）

  2. 多重集排序(图b)

    在各个节点形成的集合内除自身节点按标签升序排序（如经步骤1的图\(G\)中节点5，经过步骤2生成的多重集为(5,2-3-4)），排序的原因在于要保证结果不因邻居节点顺序改变而改变，即保证单射性。

  3. 标签压缩/标签散列(图c)

    对标签进行压缩映射，将较长的字符串映射到一个简短的标签（如利用hash编码或者继续编号等方式）；

  4. 更新标签(图d)

    将压缩映射后的新标签更新到各个节点上。

    每重复一次以上的过程，就完成一次节点自身标签与邻接节点标签的聚合。不断重复直到每个节点的label稳定不变。稳定后统计各个标签的分布，如果两个图相同标签的出现次数不一致，即可判断两个图不同构。

    伪代码如下所示：

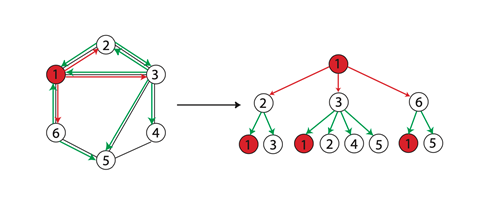
    WL-test 第 \(k\) 次迭代时节点的标号表示的是结点高度为 \(k\) 的子树结构(WL subtree)，当两个节点的\(k\)层的标签一样时，表示分别以这两个节点为根节点的WL子树是一致的。WL子树与普通子树不同，WL子树包含重复的节点。一个(根)子树是一个图的子图，它没有圈，但是有一个指定的根节点。因此，G的子树可以看作是G的不同节点的连通子集，具有一个底层的树结构。子树的高度是根节点和子树中任何其他节点之间的最大距离。所有subtree kernel都可以比较两个图中的subtree pattern，下图展示了一棵以1节点为根节点高为2的WL子树。

    再举个例子，下图中的6号、3号和5号节点的从1层到3层到WL子树分别为：

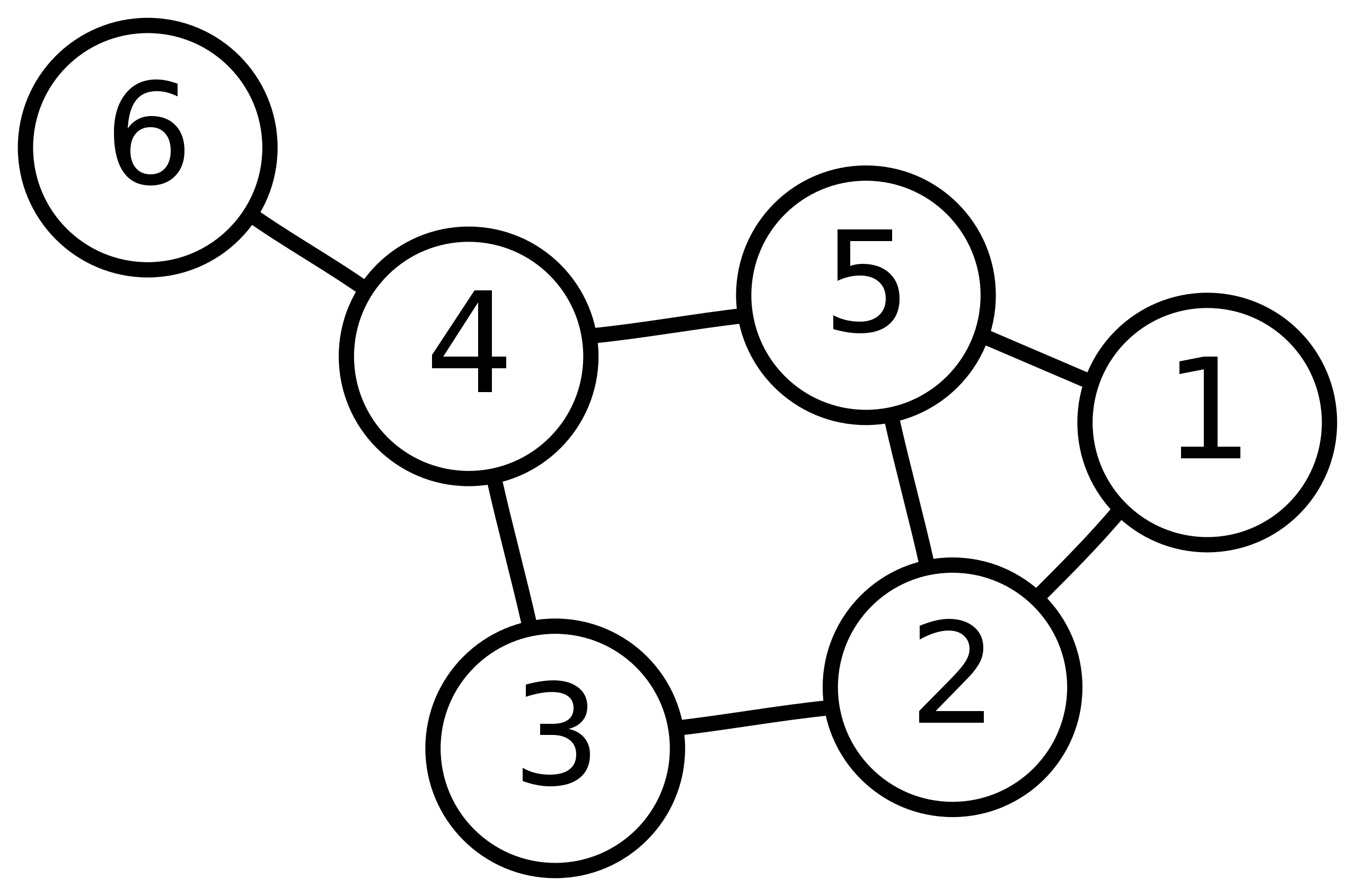
    WLsubtree案例

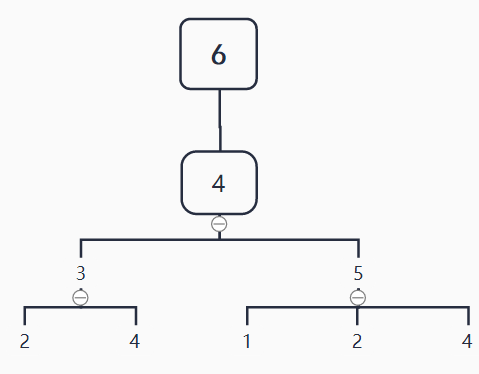
    节点6的3层WL子树：

    节点6的3层WL子树

    节点3的3层WL子树：

    节点3的3层WL子树

    节点5的3层WL子树：

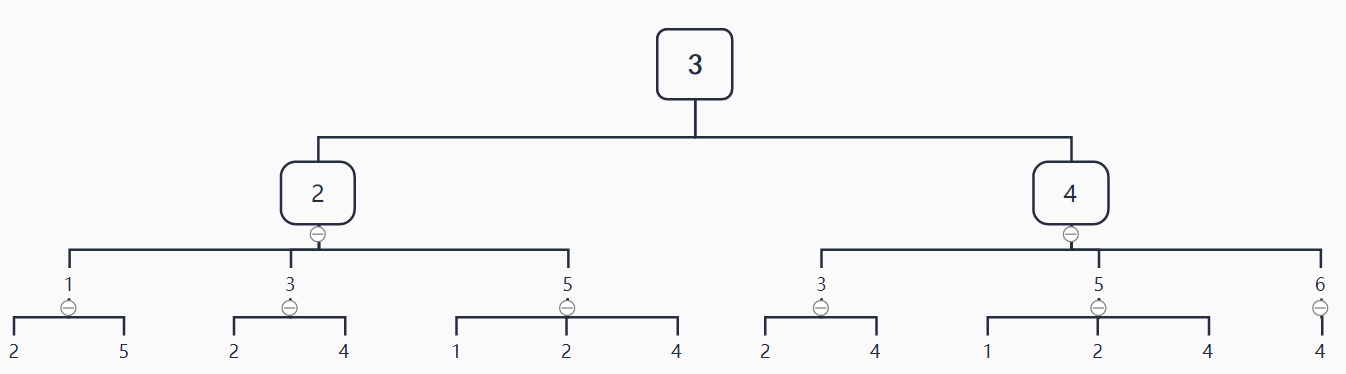
    节点3的3层WL子树

    然而WL算法只能判断两个图在k次iteration下是否同构，但无法度量图之间的相似性。进一步地，可以利用WL Subtree Kernel方法估计两个图的相似性。该方法实际上是在WL-test算法基础上增加了第五步(图e)。

  5. 迭代 1 轮后，利用计数函数分别得到两张图的计数特征，如：分别统计图中各类标签出现的次数，存于一个向量，这个向量可以作为图的表征。两个图的这样的向量的内积，即可作为这两个图的相似性的估计。

GNN与WL-test

这里的GNN实际上指的是基于消息传递图神经网络(Message Passing Neural Networks,MPNN) )架构设计的GNN模型。

复习一下，基于MPNN设计的图表示学习模型简单来说主要包括以下几个部分：

  1. 利用消息函数\(M_t\)聚合邻居特征（消息）；
  2. 利用节点更新函数\(U_t\)更新节点自身的特征。

和前面WL-test计算步骤对比可以发现，WL-test和基于MPNN设计的图神经网络模型很相似。这也是为什么很多学者提到：

从另一个角度来讲，GCN模型可以看作图上非常有名的Weisfeiler-Lehman算法的一种变形。

用GNN学习图表示（特征）

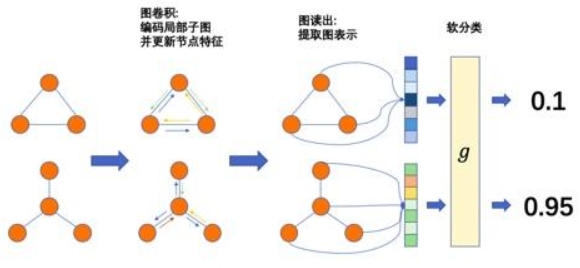
在之前的博客中，我们已经提到，基于MPNN设计的GNN模型通过以下两个步骤学习图级别的表示：

  1. 学习图中节点的表征（通过聚合和更新操作）；
  2. 对图上各个节点的表征做图池化（Graph Pooling），或称为图读出（Graph Readout）获得图级别的表示(Graph Representation)。

学习图中节点的表征

在聚合的过程中，WL test最大的特点是其聚合函数采用的是单射(injective)的hash函数。

在数学里，单射函数为一函数，其将不同的引数连接至不同的值上。更精确地说，函数f被称为是单射时，对每一值域)内的y，存在至多一个定义域内的x使得f(x) = y。百度百科-单射

如果GNNs的聚合函数是定义在multiset上的单射函数，那么GNNs和WL的表征能力一样。

图池化Graph Pooling/图读出Graph Readout

PyG中提供的可选的基于结点表征计算得到图表征的方法有：

  1. "sum"：对节点表征求和：torch_geometric.nn.glob.global_add_pool。
  2. "mean"：对节点表征求平均：torch_geometric.nn.glob.global_mean_pool
  3. "max"：对一个batch中所有节点计算节点表征各个维度的最大值：torch_geometric.nn.glob.global_max_pool。
  4. "attention"：基于Attention对节点表征加权求和： torch_geometric.nn.glob.GlobalAttention；
  5. "set2set": 另一种基于Attention对节点表征加权求和的方法： torch_geometric.nn.glob.Set2Set；

PyG中集成的所有的图池化的方法可见于Global Pooling Layers。

现有的GNN模型达不到WL-test的原因(eg.GCN、GraphSAGE)

为什么诸多 GNN 变体没有 GIN 能力强呢？主要是因为GNN 变体的聚合和池化过程不满足单射。

聚合和更新操作的选择至关重要：只有多集内射函数才能使其等同于 Weisfeiler-Lehman 算法。一些文献中常用的聚合器选择，例如，最大值或均值，实际上严格来说没有 Weisfeiler-Lehman 强大，并且无法区分非常简单的图结构：

GCN的消息传递函数（sum）：

在这里插入图片描述
在这里插入图片描述

GCN的池化函数（mean）：

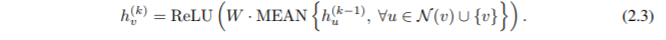
GraphSAGE的消息传递函数（mean）： \[ h_v^k←σ(W⋅MEAN({h_v^{k−1}}∪{h_u^{k−1},∀u∈N(v)})) \] GraphSAGE的池化函数（max）： \[ h^k_{\mathcal N(v)}=AGGREGATE^{pool}_k=max({σ(W_{pool}h^{k−1}_u+b),∀u∈\mathcal N(v)}) \]

\[ h^{k}_v←σ(W^k⋅CONCAT(h^{k−1}_v,h^k_{\mathcal N(v)})) \]

基于mean和max的池化函数存在一些问题，以下图为例：

设节点以颜色为标签，即 r g b。

  • 对于图 a 来说，max 和 mean 池化操作无法区分其结构，聚合邻居节点后最终标签都为 b，而对于 sum 操作来说 可以得到 2b 和 3b；
  • 对于图 b 来说，max 操作无法区分，而 mean 和 sum 可以区分；
  • 对于图 c 来说，max 和 mean 都无法区分，而 sum 依然可以区分。

由此可见，max 和 min 并不满足单射性，故其性能会比 sum 差一点。

但为什么GCN和GraphSAGE在一些任务上的效果很好呢？

文章中也给出了解释：

Mean-pooling 致力于学习节点 feature 的分布： 所以，在下述情况中，Mean也能表现的很好：

  1. 当我们的任务之和节点feature的分布有关，而与具体的局部结构无关时
  2. 当节点的具有丰富的feature，很少重复时

这就解释了为什么GCN在做节点分类时，为什么会有那么好的效果：因为每个节点的特征很难会重复。

Max-pooling 学的是 underlying set：Max处理Multiset时，只关心其对应的underlying set。所以，Max既没有学到局部结构，也没有学到分布。当我们关心Representative element或者“skeleton”时，Max会有好效果。

图同构网络架构(Graph Isomorphism Network,GIN)

GIN-学习图中节点的表征（聚合和更新操作）

原理

由前面的知识可以知道，要得到逼近WL-test结果的GNN架构的核心在于设计聚合器的单射函数。

如果我们把节点上一层的表征表示为\(c\)，其邻居的表征的集合表示为\(X\)，那么任意关于\(c\)与 \(X\) 的函数 \(g\) (当然包括单射函数) 都可以表示为\(\phi\) 与\(f\) 的复合形式。

设 \(\mathcal{X}\) 可数，那么会存在一个函数 $f:^n $ 使得对于任意有限多重集 \(X\subset \mathcal{X}\) 都有 \(h(c,X)=(1+\varepsilon)·f(c)+\sum_{x\in X}f(x)\)。则任意一个多重集函数 \(g\) 可以被分解为\(g(X)=\phi((1+\varepsilon)·f(c)+\sum_{x\in X}f(x))\)。

引入多层感知机来学习函数 \(f,\varphi\)，便可得到 GIN 最终的基于 SUM+MLP 的聚合函数： \(h_v^k = \mathbf{MLP}^k\Big((1+\varepsilon^k)\cdot h_v^{k-1} + \sum_{u\in N(v)}h_u^{k-1} \Big)\)

  • MLP 可以近似拟合任何函数；
  • 第一次迭代时，如果输入的是 One-hot 编码，在求和前不需要用 MLP，因为 Ont-hot 向量求和后依旧是单射的。

代码

卷积层设计

在节点嵌入模块中的关键组件为GINConv。我们需要复写MPNN框架中的message、aggregate和update函数以实现GIN中的卷积过程。

可以通过torch_geometric.nn.GINConv来使用PyG定义好的图同构卷积层，然而该实现不支持存在边属性的图。在这里我们自己自定义一个支持边属性的GINConv模块。

由于输入的边属性为类别型，因此我们利用BondEncoder先将类别型边属性转换为边表征。

在forward函数中执行out = self.mlp((1 + self.eps) *x + self.propagate(edge_index, x=x, edge_attr=edge_embedding))实现消息的更新。这与前面所述的公式一致。

import torch
from torch import nn
from torch_geometric.nn import MessagePassing
import torch.nn.functional as F
from ogb.graphproppred.mol_encoder import BondEncoder

### GIN convolution along the graph structure

class GINConv(MessagePassing):
    def __init__(self, emb_dim):
        '''
            emb_dim (int): node embedding dimensionality
        '''
        super(GINConv, self).__init__(aggr = "add")
        self.mlp = nn.Sequential(nn.Linear(emb_dim, emb_dim), nn.BatchNorm1d(emb_dim), nn.ReLU(), nn.Linear(emb_dim, emb_dim))
        self.eps = nn.Parameter(torch.Tensor([0]))
        self.bond_encoder = BondEncoder(emb_dim = emb_dim)

    def forward(self, x, edge_index, edge_attr):
        edge_embedding = self.bond_encoder(edge_attr) # 先将类别型边属性转换为边表征
        out = self.mlp((1 + self.eps) *x + self.propagate(edge_index, x=x, edge_attr=edge_embedding))
        return out

    def message(self, x_j, edge_attr):
        return F.relu(x_j + edge_attr)

    def update(self, aggr_out):
        return aggr_out
节点表示学习模块

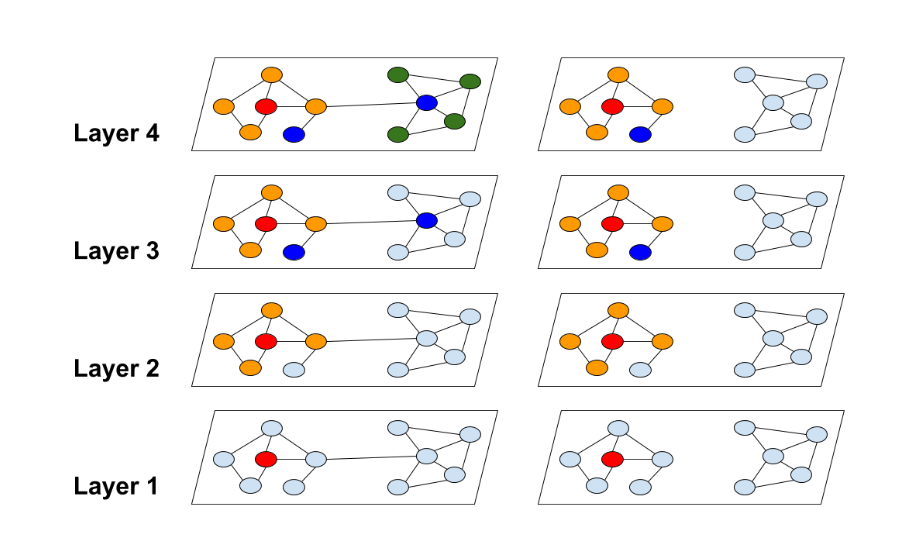
输入到此节点嵌入模块的节点属性为类别型向量，因此首先用AtomEncoder对其做嵌入得到第0层节点表征。然后逐层计算节点表征，从第1层开始到第num_layers层，每一层节点表征的计算都以上一层的节点表征h_list[layer]、边edge_index和边的属性edge_attr为输入。需要注意的是，GINConv的层数越多，此节点嵌入模块的感受野（receptive field）越大，结点i的表征最远能捕获到结点i的距离为num_layers的邻接节点的信息。

import torch
from mol_encoder import AtomEncoder
from gin_conv import GINConv
import torch.nn.functional as F

# GNN to generate node embedding
class GINNodeEmbedding(torch.nn.Module):
    """
    Output:
        node representations
    """

    def __init__(self, num_layers, emb_dim, drop_ratio=0.5, JK="last", residual=False):
        """GIN Node Embedding Module"""

        super(GINNodeEmbedding, self).__init__()
        # num_layers (int, optional): number of GINConv layers. Defaults to 5.
        self.num_layers = num_layers
        self.drop_ratio = drop_ratio
        self.JK = JK
        # add residual connection or not
        self.residual = residual

        if self.num_layers < 2:
            raise ValueError("Number of GNN layers must be greater than 1.")
		# emb_dim (int, optional): dimension of node embedding. Defaults to 300.
        self.atom_encoder = AtomEncoder(emb_dim)# 先将类别型节点属性转化为节点表征

        # List of GNNs
        self.convs = torch.nn.ModuleList()
        self.batch_norms = torch.nn.ModuleList()

        for layer in range(num_layers):
            self.convs.append(GINConv(emb_dim))
            self.batch_norms.append(torch.nn.BatchNorm1d(emb_dim))

    def forward(self, batched_data):
        x, edge_index, edge_attr = batched_data.x, batched_data.edge_index, batched_data.edge_attr

        # computing input node embedding
        h_list = [self.atom_encoder(x)]  # 先将类别型节点属性转化为节点表征
        for layer in range(self.num_layers):
            h = self.convs[layer](h_list[layer], edge_index, edge_attr)
            h = self.batch_norms[layer](h)
            if layer == self.num_layers - 1:
                # remove relu for the last layer
                h = F.dropout(h, self.drop_ratio, training=self.training)
            else:
                h = F.dropout(F.relu(h), self.drop_ratio, training=self.training)

            if self.residual:
                h += h_list[layer]

            h_list.append(h)

        # Different implementations of Jk-concat
        # JK (str, optional): 可选的值为"last"和"sum"。选"last"，只取最后一层的结点的嵌入，选"sum"对各层的结点的嵌入求和。Defaults to "last".
        if self.JK == "last":
            node_representation = h_list[-1]
        elif self.JK == "sum":
            node_representation = 0
            for layer in range(self.num_layers + 1):
                node_representation += h_list[layer]

        return node_representation

AtomEncoder 与 BondEncoder

当节点和边的属性都为离散值时，它们属于不同的空间，无法直接将它们融合在一起。通过嵌入（Embedding），可以将节点属性和边属性分别映射到一个新的空间，在这个新的空间中，就可以对节点和边进行信息融合。从而在GINConv中，message()函数中的x_j + edge_attr 操作可以执行节点信息和边信息的融合。

接下来，通过下方的代码中的AtomEncoder类，来分析将节点属性映射到一个新的空间是如何实现的：

  • full_atom_feature_dims 是一个链表list，存储了节点属性向量每一维可能取值的数量，即X[i] 可能的取值一共有full_atom_feature_dims[i]种情况，X为节点属性；
  • 节点属性有多少维，那么就需要有多少个嵌入函数，通过调用torch.nn.Embedding(dim, emb_dim)可以实例化一个嵌入函数；
  • torch.nn.Embedding(dim, emb_dim)，第一个参数dim为被嵌入数据可能取值的数量，第一个参数emb_dim为要映射到的空间的维度。得到的嵌入函数接受一个大于0小于dim的数，输出一个维度为emb_dim的向量。嵌入函数也包含可训练参数，通过对神经网络的训练，嵌入函数的输出值能够表达不同输入值之间的相似性。
  • 在forward()函数中，对不同属性值得到的不同嵌入向量进行了相加操作，实现了将节点的的不同属性融合在一起。

BondEncoder类与AtomEncoder类是类似的。利用ogb封装好的PygGraphPropPredDataset类，导入ogbg-molhi数据集来进行节点和边属性嵌入特征获取的实验：

import torch
from ogb.utils.features import get_atom_feature_dims, get_bond_feature_dims 

full_atom_feature_dims = get_atom_feature_dims()
full_bond_feature_dims = get_bond_feature_dims()

class AtomEncoder(torch.nn.Module):

    def __init__(self, emb_dim):
        super(AtomEncoder, self).__init__()
        
        self.atom_embedding_list = torch.nn.ModuleList()

        for i, dim in enumerate(full_atom_feature_dims):
            emb = torch.nn.Embedding(dim, emb_dim)
            torch.nn.init.xavier_uniform_(emb.weight.data)
            self.atom_embedding_list.append(emb)

    def forward(self, x):
        x_embedding = 0
        for i in range(x.shape[1]):
            x_embedding += self.atom_embedding_list[i](x[:,i])

        return x_embedding

class BondEncoder(torch.nn.Module):
    
    def __init__(self, emb_dim):
        super(BondEncoder, self).__init__()
        
        self.bond_embedding_list = torch.nn.ModuleList()

        for i, dim in enumerate(full_bond_feature_dims):
            emb = torch.nn.Embedding(dim, emb_dim)
            torch.nn.init.xavier_uniform_(emb.weight.data)
            self.bond_embedding_list.append(emb)

    def forward(self, edge_attr):
        bond_embedding = 0
        for i in range(edge_attr.shape[1]):
            bond_embedding += self.bond_embedding_list[i](edge_attr[:,i])

        return bond_embedding   

if __name__ == '__main__':
    from ogb.graphproppred.dataset_pyg import PygGraphPropPredDataset
    dataset = PygGraphPropPredDataset(name = 'ogbg-molhiv')
    atom_enc = AtomEncoder(100)
    bond_enc = BondEncoder(100)

    print(atom_enc(dataset[0].x))
    print(bond_enc(dataset[0].edge_attr))

GIN-图池化Graph Pooling/图读出Graph Readout

原理

GIN中的READOUT 函数为 SUM函数，通过对每次迭代得到的所有节点的特征求和得到该轮迭代的图特征，再拼接起每一轮迭代的图特征来得到最终的图特征： \[ h_{G} = \text{CONCAT}(\text{READOUT}\left(\{h_{v}^{(k)}|v\in G\}\right)|k=0,1,\cdots, K) \] 采用拼接每一轮迭代的图特征而不是相加的原因在于不同层节点的表征属于不同的特征空间。这样得到的图的表示与WL Subtree Kernel得到的图的表征是等价的。

代码

首先采用GINNodeEmbedding模块对图上每一个节点做节点嵌入（Node Embedding），得到节点表征；然后对节点表征做图池化得到图的表征；最后用一层线性变换对图表征转换为对图的预测。

import torch
from torch import nn
from torch_geometric.nn import global_add_pool, global_mean_pool, global_max_pool, GlobalAttention, Set2Set
from gin_node import GINNodeEmbedding

class GINGraphRepr(nn.Module):

    def __init__(self, num_tasks=1, num_layers=5, emb_dim=300, residual=False, drop_ratio=0, JK="last", graph_pooling="sum"):
        """GIN Graph Pooling Module
        Args:
            num_tasks (int, optional): number of labels to be predicted. Defaults to 1 (控制了图表征的维度，dimension of graph representation).
            num_layers (int, optional): number of GINConv layers. Defaults to 5.
            emb_dim (int, optional): dimension of node embedding. Defaults to 300.
            residual (bool, optional): adding residual connection or not. Defaults to False.
            drop_ratio (float, optional): dropout rate. Defaults to 0.
            JK (str, optional): 可选的值为"last"和"sum"。选"last"，只取最后一层的结点的嵌入，选"sum"对各层的结点的嵌入求和。Defaults to "last".
            graph_pooling (str, optional): pooling method of node embedding. 可选的值为"sum"，"mean"，"max"，"attention"和"set2set"。 Defaults to "sum".

        Out:
            graph representation
        """
        super(GINGraphPooling, self).__init__()

        self.num_layers = num_layers
        self.drop_ratio = drop_ratio
        self.JK = JK
        self.emb_dim = emb_dim
        self.num_tasks = num_tasks

        if self.num_layers < 2:
            raise ValueError("Number of GNN layers must be greater than 1.")

        self.gnn_node = GINNodeEmbedding(num_layers, emb_dim, JK=JK, drop_ratio=drop_ratio, residual=residual)

        # Pooling function to generate whole-graph embeddings
        if graph_pooling == "sum":
            self.pool = global_add_pool
        elif graph_pooling == "mean":
            self.pool = global_mean_pool
        elif graph_pooling == "max":
            self.pool = global_max_pool
        elif graph_pooling == "attention":
            self.pool = GlobalAttention(gate_nn=nn.Sequential(
                nn.Linear(emb_dim, emb_dim), nn.BatchNorm1d(emb_dim), nn.ReLU(), nn.Linear(emb_dim, 1)))
        elif graph_pooling == "set2set":
            self.pool = Set2Set(emb_dim, processing_steps=2)
        else:
            raise ValueError("Invalid graph pooling type.")

        if graph_pooling == "set2set":
            self.graph_pred_linear = nn.Linear(2*self.emb_dim, self.num_tasks)
        else:
            self.graph_pred_linear = nn.Linear(self.emb_dim, self.num_tasks)

    def forward(self, batched_data):
        h_node = self.gnn_node(batched_data)

        h_graph = self.pool(h_node, batched_data.batch)
        output = self.graph_pred_linear(h_graph)

        if self.training:
            return output
        else:
            # At inference time, relu is applied to output to ensure positivity
            # 因为预测目标的取值范围就在 (0, 50] 内
            return torch.clamp(output, min=0, max=50)

完整代码

Task8-GIN

参考文献

基于图神经网络的图表征学习方法

How Powerful are Graph Neural Networks?

【GNN】WL-test：GNN 的性能上界

Weisfeiler-Lehman算法测试图同构

图神经网络的表达能力与Weisfeiler-Lehman测试

Weisfeiler-Lehman算法测试图同构

斯坦福ICLR2019图网络最新论文：图神经网络的表征能力有多强？

【Graph Neural Network】GraphSAGE: 算法原理，实现和应用

[论文笔记]：GraphSAGE：Inductive Representation Learning on Large Graphs 论文详解 NIPS 2017

图神经网络总结（GCN/GAT/GraphSAGE/DeepWalk/TransE）

图神经网络将成AI下一拐点！MIT斯坦福一文综述GNN到底有多强

Weisfeiler-Lehman Graph Kernels