Transformer相关——（3）Attention机制

引言

这篇我们来总结一下attention机制。

Attention的直观理解

与人类对外界事物的观察机制很类似，在某种情景下（根据不同的任务可能关注点不同）我们注意力会集中在这张图片的一个区域内，而其他的信息受关注度会相应降低。Attention机制让神经网络更聚焦于对那些对最终任务有帮助的部分。比如下图的各个子图中，模型对句子下划线部分更加关注（越亮）。

再举NLP中的一个例子来说，我们在做阅读理解时，文中隐藏需要回答问题的答案的关键词/句更加关注，神经网络通过attention机制试图寻找问题答案的时候关注哪些方面。

Attention机制/模块

Attention的实质是加权求和。通过一个额外的神经网络层，用于选择输入的某些部分或者给输入的不同部分分配不同的权重。这个权是通过计算向量之间的相关性进行度量的。

我个人理解来看，可以直观理解attention是一种不规则的感受野，对整张图像或者整篇文档都有感知，且在局部重点感知。

Attention机制分类（了解）

按可微性分

Hard-attention

0/1问题，被attention的输入部分被选择，否则不关注不选择（不参与计算）。Hard-attention是一个随机预测的过程，更关注点，强调动态变化。不可微，训练过程往往通过强化学习完成。

Soft-attention

[0，1]连续分布，每个区域被关注的程度高低，用0~1的score表示。Soft-attention更关注区域或者通道，是确定性的注意力，可以直接通过网络学习生成，可微。

按关注域分

空间域spatial domain

通道域channel domain

层域layer domain

混合域mixed domain

时间域time domain

Attention解决了什么问题

上一篇提到，基础Seq2Seq模型存在以下三种问题：

中间语义向量$C$无法完全表达整个输入序列的信息；

中间语义向量$C$对$y_1,y_2...y_{n-1}$所产生的贡献都是一样的；

随着输入信息长度的增加，先前编码好的信息会被后来的信息覆盖，丢失很多信息。

attention机制就可以用于解决上述问题。接下来说明attention机制如何解决这些问题。

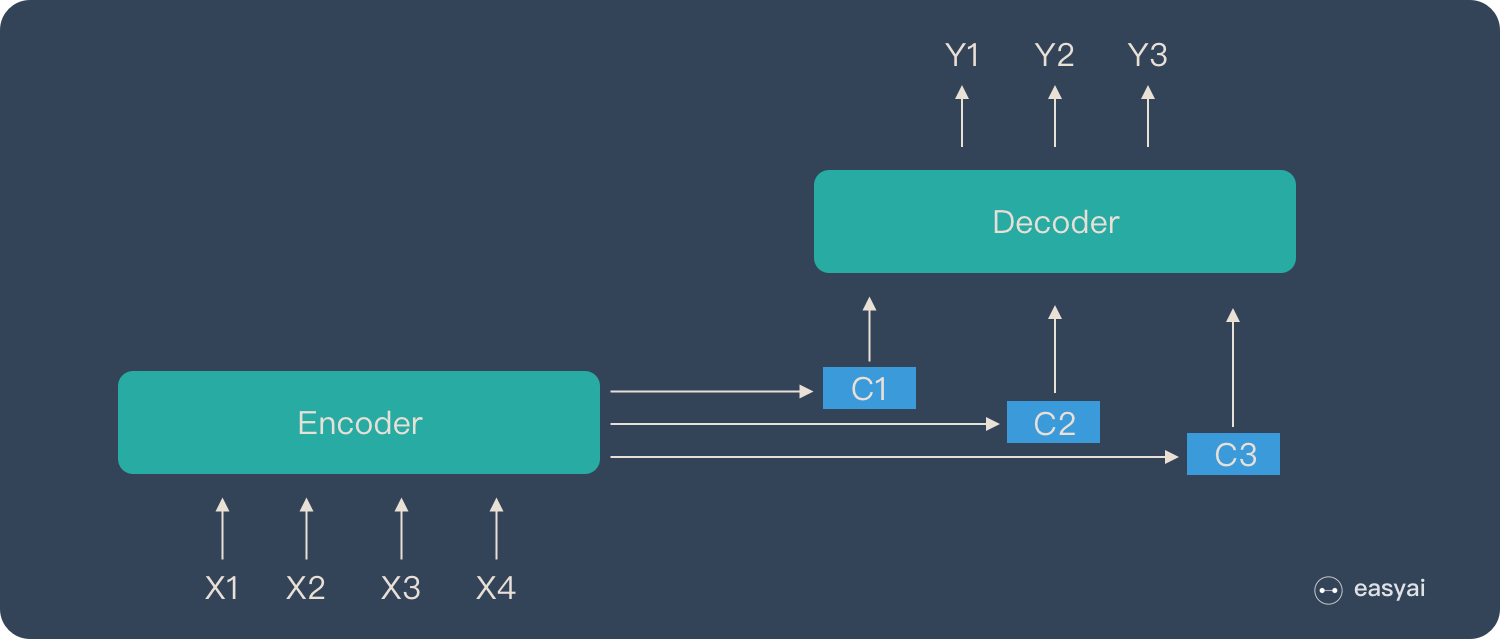
引入Attention机制的Seq2Seq模型

如果一个输出句有N个文字，就会产生N个context vector，一一对应（下图中为$C_1,C_2,C_3$），$C_i$考虑一整个Sequence的信息，且对于每个输出来说，会对输入的序列有不同的侧重（找到对于每个输出来说一整个Sequence中哪些部分更加重要）。

`context vector`计算流程（Attention机制流程）

注意力机制可以分为三步：

信息输入；
（核心）计算attention score（注意力权重） $\mathbf α$，衡量了输入句中的每个文字对目标句中的每个文字所带来重要性的程度；
一般可以接一个softmax对这些权重进行归一化，也可以使用ReLU等激活函数；
计算输入信息的加权平均。

这里引用一个我觉得写的最好的Attention机制的解释，来源于从Encoder-Decoder(Seq2Seq)理解Attention的本质：

Attention机制：将Source中的构成元素想象成是由一系列的(Key,Value)数据对构成，此时给定Target中的某个元素Query，通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数，然后对Value进行加权求和，即得到了最终的Attention数值。所以本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。即可以将其本质思想改写为如下公式： \[ Attention(Query_j,Source)=\sum_{i=1}^{N}Similarity(Query_j,Key_i)∗Value_i \]

Query就像是你搜寻引擎的时候，去搜寻相关文章发出的问题。而Key、Value就像搜索时被检索的关键词和内容。也就是说，计算Attention score像是计算这个Source中的各个部分（各个检索结果的Key、Value）能多大程度上回答这个Query。

请仔细理解上述表达中Query、Key、Value之间的关系，这对自己利用Attention机制去设计模型有很大的帮助（在明确需要获得什么对什么的attention时，更好地知道哪个向量作为Query，哪个作为Key，哪个为Value），后半部分还会介绍几种attention机制的变形，可以注意一下Q、K、V分别代表了什么。

接下来我们先来说核心的注意力权重/attention score的计算方法，也就是如何计算$Similarity(Query_j,Key_i)$。

计算`attention score`

前面提到，Attention的实质是加权求和，权是通过计算向量之间的相关性进行度量的。

那么根据不同的相关性计算方式，可以有不同的attention score($α$)计算方式，目前有以下几种方式：

加性additive相关性：$α_{i,j}=Wtanh(q^i+k^j)$
点积dot product相关性（最常见）：$α_{i,j}=q^i·k^j$，比加性相关性计算更快。
缩放点积相关性（Transformer中使用）：$α_{i,j}=\frac{(q^i·k^j)}{\sqrt{d}}$，$d$是输入信息的维度。向量的点积结果会很大，将softmax函数push到梯度很小的区域，scaled会缓解这种现象。缩放点积相关性可以让attention score的均值和方差和q、k相同，有利于缓解梯度消失。具体可参考：transformer中的attention为什么scaled? - TniL的回答

P.S.该回答评论区有一条很有意思的回复：

一篇将transformer用在NER任务上的文章argue：在NER任务上attention scaled可能不好(因为attention scaled，即除以$\sqrt{d_k}$让整个attention变smooth了，而NER任务中可能只需要attend特定的word，变平滑的attention可能引入更多噪声)，所以它把除以$\sqrt{d_k}$这步去掉了，使得最后的attention比较sparse(也就是这里提到的softmax后接近于one-hot)。

总之选择什么样的相关性计算attention score还是得看下游任务~
双线性相关性：$α_{i,j}=q^i·W·k^j$

那么Q、K、V怎么来呢？（信息输入）

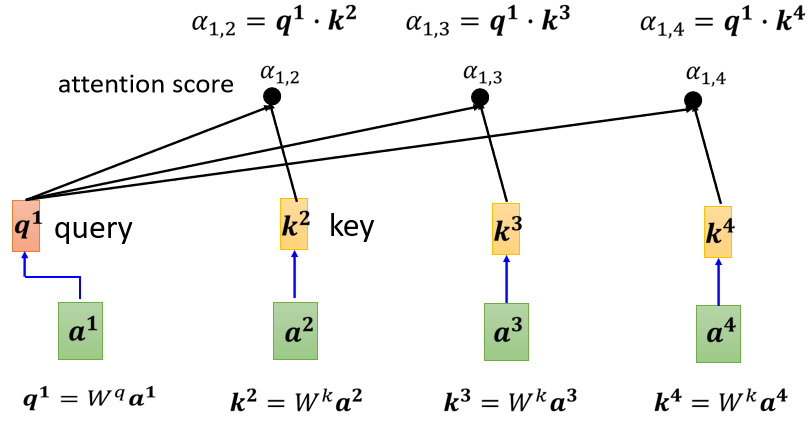
我们在进行Attention score计算时，往往不直接使用原始特征向量$X_1,X_2,...$，而是分别使用三个权重（$W^q,W^k,W^v$）对原始特征向量进行线性变换后，分别作为Q、K、V。$W^q,W^k,W^v$就是在训练过程中需要学习的参数。

如下图示例了$Q=[q_1,q_2,...,q_N]$的计算方式，特别注意的是，Q、K、V线性变换矩阵通常不同（$W^q≠W^k≠W^v$），但对于输入序列中的每一列（比如句子中的每一个词）来说，所用的$W^q$是一样的。

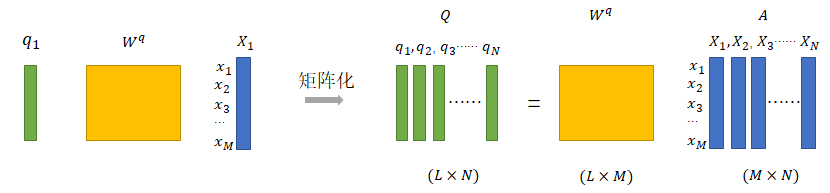
同理可根据模型对输入信息进行线性变化以获得K和V。

计算attention输出矩阵

根据不同相关性的计算方法，我们利用$Q$和$K$计算attention score，此时只计算了相关性权重，还需要对输入信息进行加权求和得到attention输出矩阵： \[ att(q,V)=\sum_{i=1}^{N}\alpha_iV_i \] 完整来看，当矩阵特征向量以列向量形式表示时(也是上图中的情况)，attention的输出矩阵可以按照下述公式计算（以缩放点积相关性+softmax为例）： \[ Attention(Q,K,V)=Vsoftmax(\frac{K^TQ}{\sqrt{d_k}}) \] 当矩阵特征向量以行向量形式表示时，attention的输出矩阵可以按照下述公式计算（以缩放点积相关性+softmax为例）： \[ Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V \] 上面说完了attention机制的核心是如何计算的，但事实上还有下面两个问题没有说得特别清楚，关系到如何在模型中加入attention机制。

Q、K、V怎么设定？（其实还是Q、K、V怎么来的问题，要分别用哪个特征矩阵$X$变换获得呢？）
attention的输出矩阵怎么和模型其他层结合？

事实上在不同的模型中attention机制存在不同的变种，输出矩阵和模型其他层结合的方式也不同。接下来将详细说明Seq2Seq模型中的attention机制以及介绍transformer中使用的self-attention机制，进一步解答上面两个问题。

Seq2Seq模型中的attention机制

Attention机制在Seq2Seq模型中如何应用的？

下面两个示意图可以帮助理解Attention机制在Seq2Seq模型中是如何应用的。

可以看到，在Seq2Seq模型中attention机制中：

将前一个输出$s_j$作为Query，encoder中RNN模块编码的各个隐藏图层$h_0,h_1,...h_n$作为key和value进行attention；
输出的矩阵作为$context\space C_j$与前一个输出$s_j$拼接$s_j,C_j$作为求下一个输出$s_{j+1}$RNN模块的输入。

Seq2Seq中的attention机制有什么问题？

可以发现，Seq2Seq中attention机制将输入句子和生成句子之间进行attention，且下一个输出依赖上一个句子和上一个输出的结果。这种形式存在两个问题：

是串行的，存在无法并行化的问题，导致计算速度很慢；
关注句子和句子间的特征，没有关注句子内部的信息（如语法特征、短语结构等）。

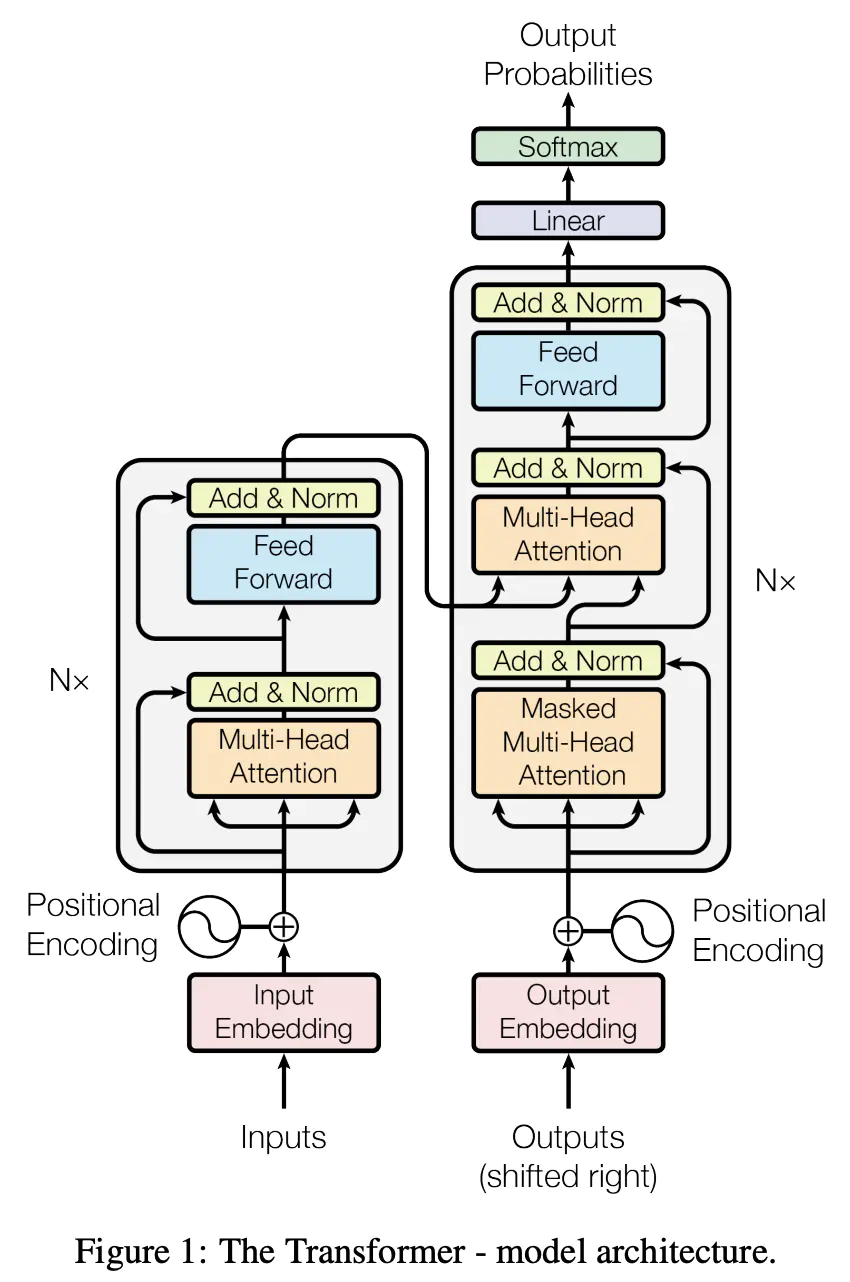
Transformer中的self-attention机制

前面提到Seq2Seq中的attention机制存在的两个问题可以用self-attention机制解决。这里我们只介绍Transformer中self-attention机制的原理，在Transformer中self-attention机制是如何与其他层结合的等下次博客再整体串讲。

self-attention

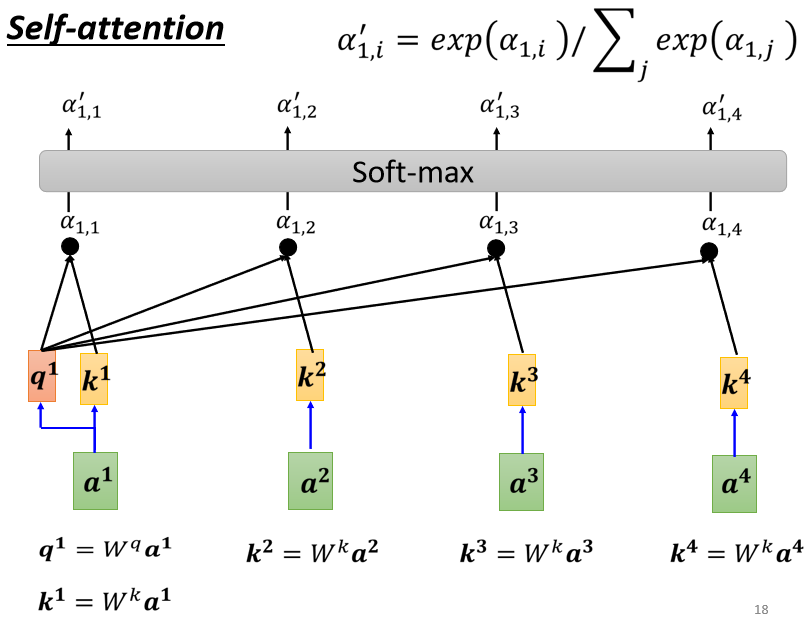
我们前面说了attention机制的通用形式，其中Q、K、V如何选择其实就影响了attention输出矩阵的表达，self-attention顾名思义就是对自己进行attention，其Q、K、V都是用同一个输入矩阵$X$，然后分别用三个不同矩阵（$W^q,W^k,W^v$）做一步线性变换得到的。

self-attention的计算过程如下图所示：

举个NLP的例子来看，self-attention机制建立了单词和整个句子的attention关系，可以学习到句子内部的信息；此外，self-attention是支持并行的，在计算每个单词的attention时互不影响，但也因此损失了句子内部单词之间的位置信息。

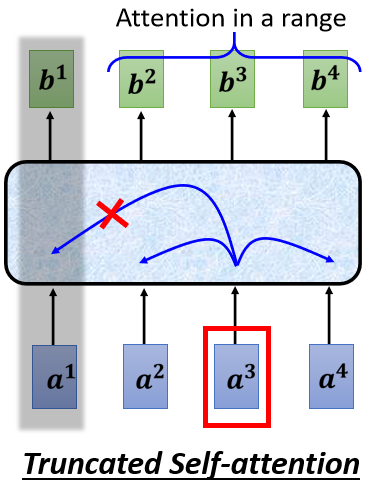
Truncated self-attention

输入序列的长度为$N$，self-attention计算的attention score大小为$N×N$，在面对超长文本或者语音时，self-attention的计算量非常大，需要的内存也很大。

这个时候可以使用Truncated self-attention，相当于仅考虑一个窗口内的文本或者语音做attention，可以加快运算的速度。

Multi-head self-attention

事实上，在Transformer中使用的是self-attention的进阶版本，Multi-head self-attention多头自注意力机制。

多头 attention 注意力机制直观理解为，相关这件事情有很多种不同的形式，有很多种不同的定义的相关性，或许应该不同的$Q$负责不同种类的相关性，从而能够关注来自不同位置的不同表示子空间的信息。但是，没有机制可以保证不同的 attention 头一定可以捕捉到不同的特征。

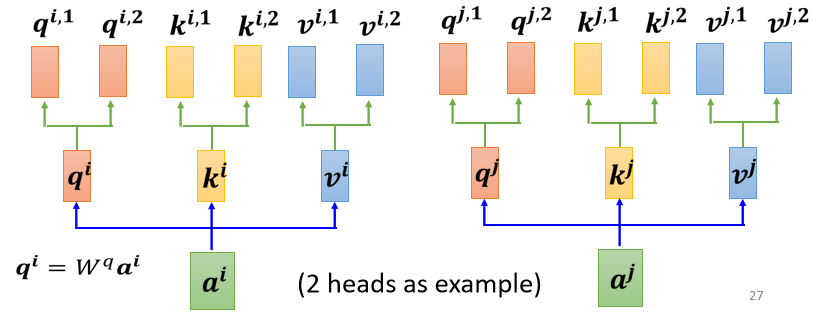
如下图所示，对原始序列矩阵$X$，假设有8个head的self-attention，分别乘上8个组各自的$W_i^q,W_i^k,W_i^v$，得到8个组各自的Q、K、V，再分别在8个组内各自计算attention score和attention的输出，拼接8个head的attention的输出，再用一个线性变换矩阵$W^O$得到最终的多头attention输出。

这里也补充一个李宏毅老师的多头自注意力机制的介绍，与上述不同的是，李宏毅老师讲解中的多头注意力机制首先把$X$经过一个$W^q$得到$Q$，然后再乘上另外n个（head数）矩阵对$Q$进行分解，再进行attention score和输出矩阵的计算。

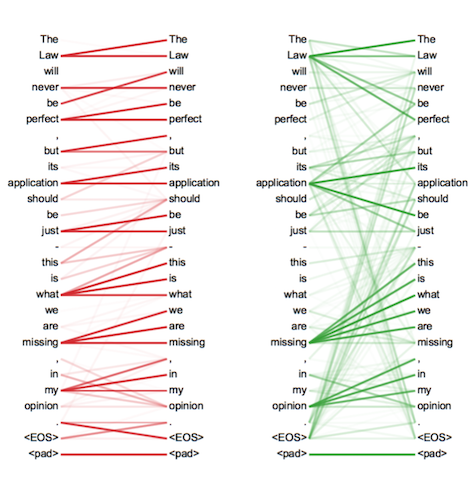
下图展示了NLP中的一个双头注意力机制的可视化结果。

TIPS

这里需要注意的是，多头注意力机制中往往满足：self-attention的隐藏层维度（$hidden\_emb\_dim$）*$n\_heads$=输入特征（经过线性变换）的维度($emb\_dim$)，然后$W^O$的维度为$emb\_dim$。那么可能会问为什么不令$hidden\_emb\_dim$=$emb\_dim$，$W^O$的维度为$emb\_dim*n\_heads$呢（看上去似乎也能进行计算）？

答案摘自：BERT中，multi-head 7686412与直接使用768*768矩阵统一计算，有什么区别？

照我们的直观想象（以及事后的一些观察），我们可以发现每个token通常只是注意到有限的若干个token，这说明Attention矩阵通常来说是很“稀疏”的（这个稀疏指的是很多概率值非常接近于0，而不是等于0，因为softmax的结果理论上不能严格等于0），而稀疏意味着我们就算降到 $Q,K\in\mathbb{R}^{512\times 512}$ 也是一种浪费，它可能只是两个更低维矩阵的乘积，即所谓的低秩分解。

self-attention的优势和缺点

优势：

并行 Multi-Head Attention 和 CNN 一样不依赖前一时刻的计算，可以很好的并行，优于 RNN。

长距离依赖 优于 Self-Attention 是每个词和所有词计算 Attention，所以不管他们中间有多长距离，最大路径长度都只是 1，可以捕获长距离依赖关系。

缺点：

损失了句子内部单词之间的位置信息；
运算量很大。

self-attention和CNN、RNN的关系

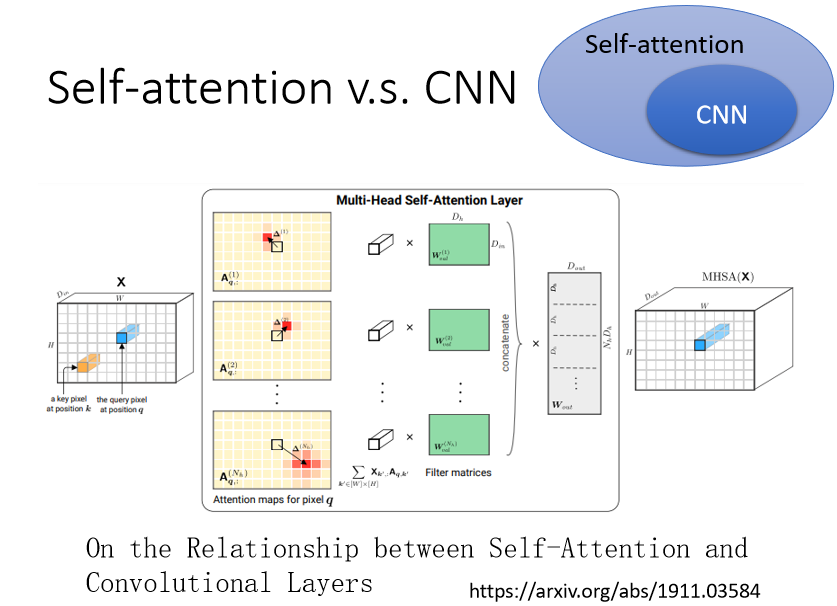
self-attention v.s. CNN

CNN 可以看作是一种简化版的 Self-attention，是Self-attention 的特例，CNN的卷积核对信息获取范围做了限制，只能获得卷积核内（receptive field）里面的信息，而在做 Self-attention 的时候，考虑了整张图片的信息； receptive field 的范围跟大小，是人决定的。
Self-attention 是一个复杂化的 CNN，用 attention去找出重要的的 pixel，就像 receptive field 是自动学习的，network自己学习到receptive field 的形状，以某个 pixel 為中心,哪些 pixel 是重要的需要被考虑的。

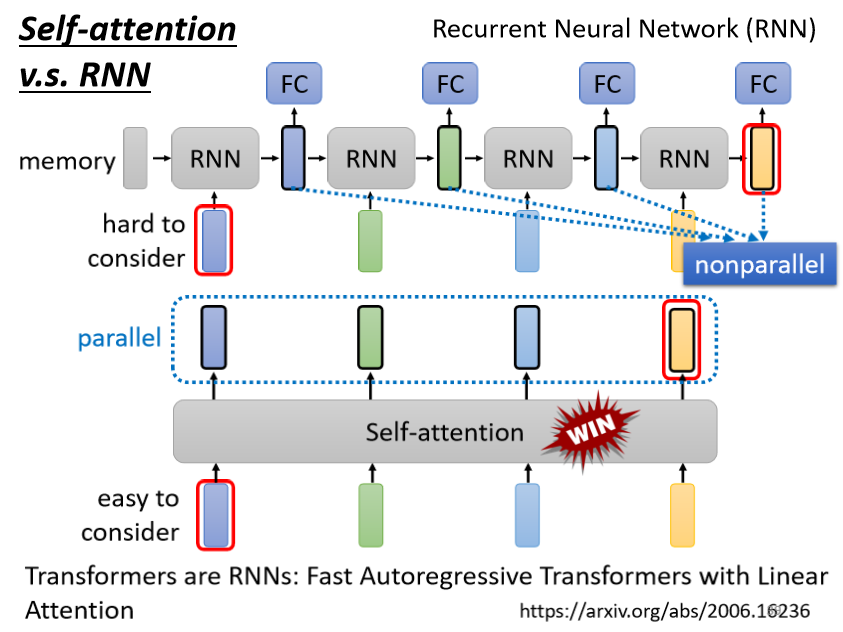
self-attention v.s. RNN

前面也提到Self-attention是可并行化的，而RNN依赖于上一个输出，是串行机制，所以在运算速度上，Self-attention 比 RNN 更有效率。

此外RNN模块即使是双向的RNN、加上了门控机制的RNN模型，对很长序列距离当前RNN模块很远的RNN模块信息很可能被遗忘或稀释了，丢失很多信息，而self-attention可以从非常远的 vector，在整个 sequence 上轻易地抽取信息。

很多的应用都往往把 RNN 的架构，逐渐改成 Self-attention 的架构了。

Self-attention对不同数据的应用场景

核心思想：对vector集合就可以做self-attention。

语音：

前面举到了Self-attention在NLP中的案例，它还可以应用到语音领域，将声音频谱编码成vector；
图像：

可以将同一个像素不同channel的值看成一个vector，应用attention机制：
graph：

node有node embedding，组成了vector set，可以用self-attention。

特别地，在网络中存在edge信息，指示了哪些 node 之间是相连的，那么只计算有 edge 相连的 node 就可以，即如果两个 node 之间没有关系，则不需要再去计算它的 attention score，直接设置为0。