Pytorch与视觉竞赛入门2.1-PyTorch激活函数原理和使用

PyTorch激活函数原理和使用

参考资料：GELU 激活函数

Pytorch激活函数及优缺点比较

torch.nn.GELU

\[ GELU(x)=xP(X<=x)=xΦ(x) \]

这里$Φ ( x ) \(是正太分布的概率函数，可以简单采用正太分布\)N ( 0 , 1 )\(要，或者使用参数化的正太分布\)N ( μ , σ )$ ，然后通过训练得到\(μ\)。

对于假设为标准正太分布的\(GELU(x)\)，论文中提供了近似计算的数学公式，如下： \[ GELU(x) = 0.5x(1+tanh[\sqrt{2/\pi}(x+0.044715x^3)]) \] bert源码给出的GELU代码pytorch版本表示如下：

def gelu(input_tensor):
	cdf = 0.5 * (1.0 + torch.erf(input_tensor / torch.sqrt(2.0)))
	return input_tesnsor*cdf

\[ erf(x)= \frac{2}{π}∫_0^xe^{−t^2}dt \]

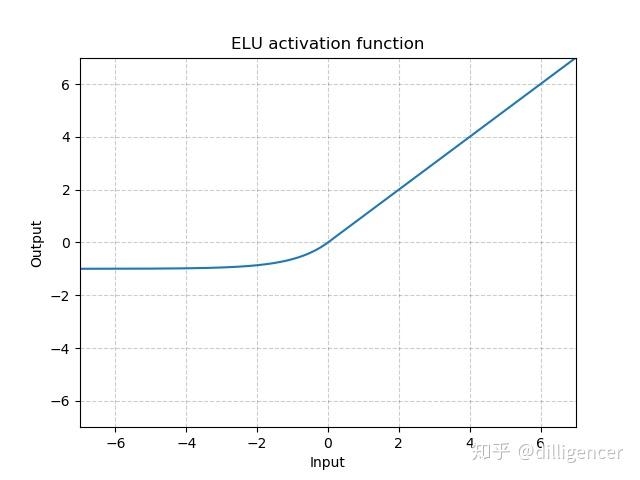
torch.nn.ELU(alpha=1.0,inplace=False)

def elu(x,alpha=1.0,inplace=False):
    return max(0,x)+min(0,alpha∗(exp(x)−1))

α是超参数，默认为1.0

img
img

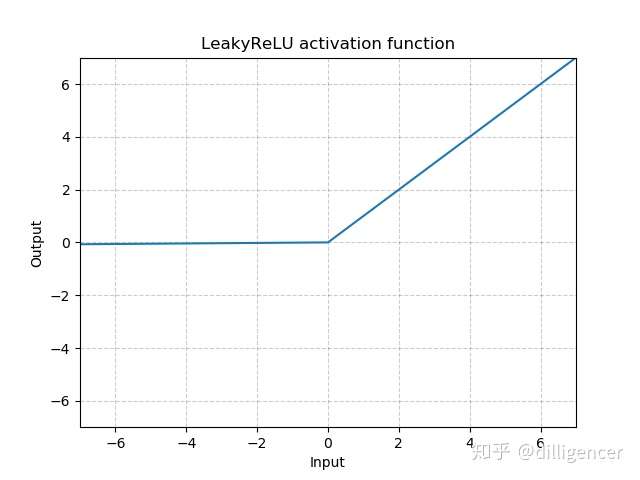
torch.nn.LeakyReLU(negative_slope=0.01,inplace=False)

def LeakyReLU(x,negative_slope=0.01,inplace=False):
    return max(0,x)+negative_slope∗min(0,x)

其中 negative_slope是超参数，控制x为负数时斜率的角度，默认为1e-2

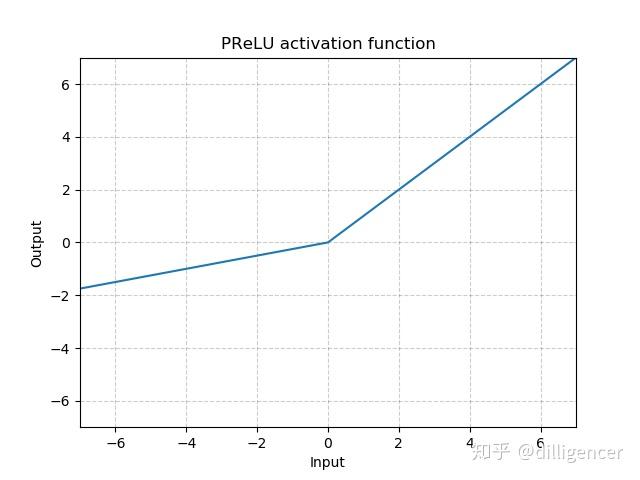
torch.nn.PReLU(num_parameters=1,init=0.25)

def PReLU(x,num_parameters=1,init=0.25):
    return max(0,x)+init∗min(0,x)

其中a 是一个可学习的参数，当不带参数调用时，即nn.PReLU()，在所有的输入通道上使用同一个a，当带参数调用时，即nn.PReLU(nChannels)，在每一个通道上学习一个单独的a。

注意：当为了获得好的performance学习一个a时，不要使用weight decay。

num_parameters：要学习的a的个数，默认1

init：a的初始值，默认0.25

torch.nn.ReLU(inplace=False)

CNN中最常用ReLu。

def ReLU(x,inplace=False):
    return max(0,x)

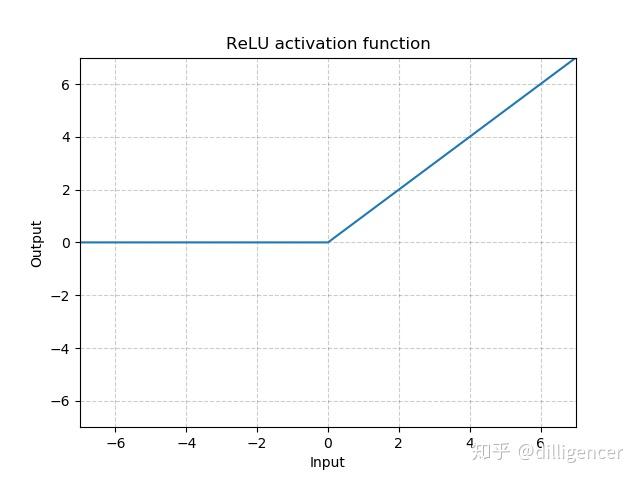
torch.nn.ReLU6(inplace=False)

def ReLU6(x,inplace=False):
    return min(max(0,x),6)

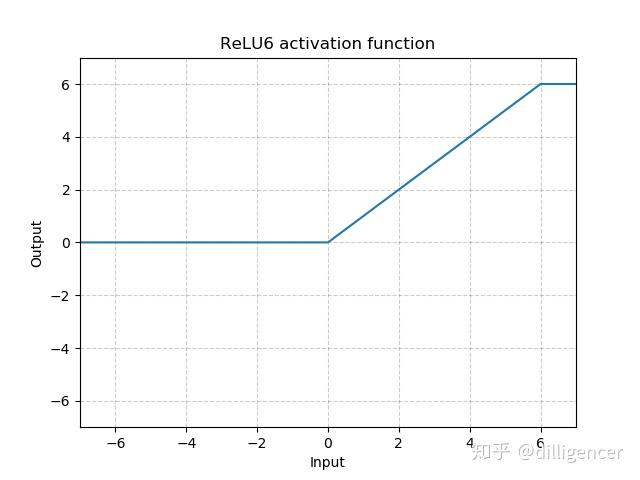
torch.nn.SELU(inplace=False)

def SELU(x,inplace=False):
    alpha=1.6732632423543772848170429916717
	scale=1.0507009873554804934193349852946
    return scale∗(max(0,*x*)+min(0,alpha∗(exp(x)−1)))

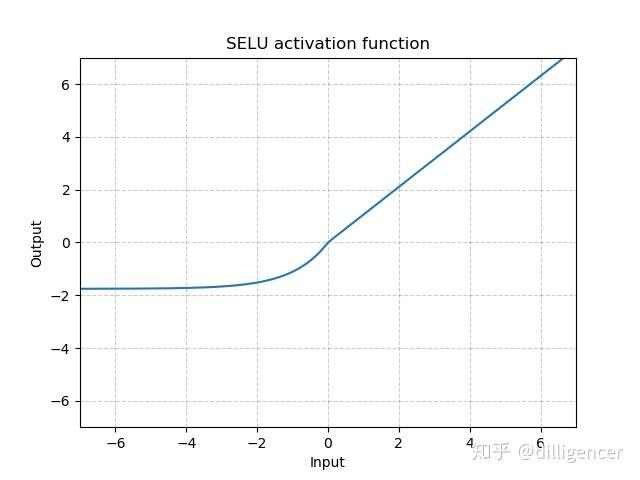
torch.nn.CELU(alpha=1.0,inplace=False)

def CELU(x,alpha=1.0,inplace=False):
    return max(0,x)+min(0,alpha∗(exp(x/alpha)−1))

其中α 默认为1.0

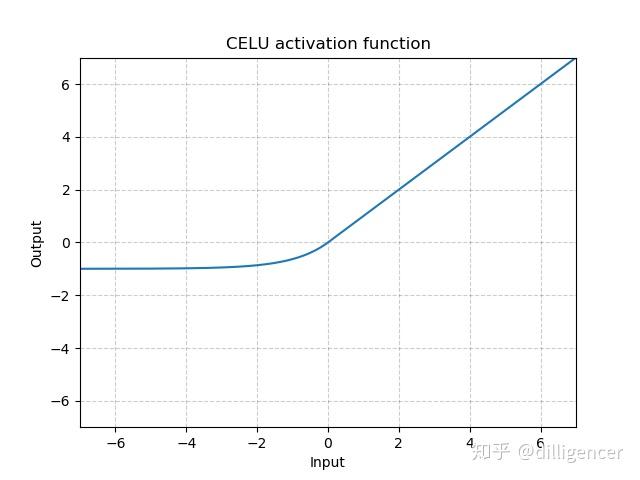
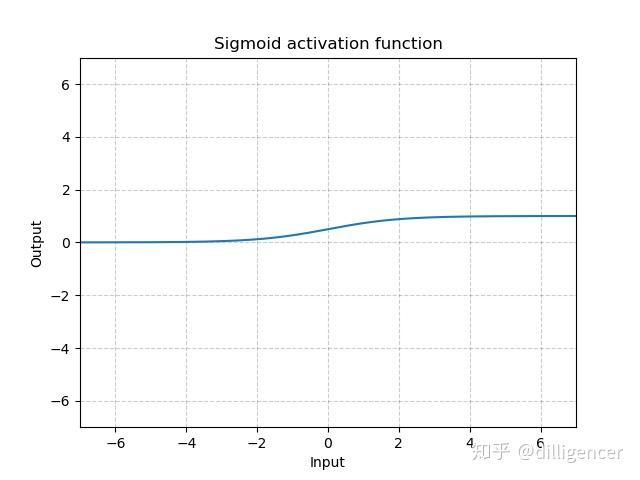
torch.nn.Sigmoid

\[ Sigmoid(x)=\frac{1}{1+exp(-x)} \]

def Sigmoid(x):
    return 1/(np.exp(-x)+1)

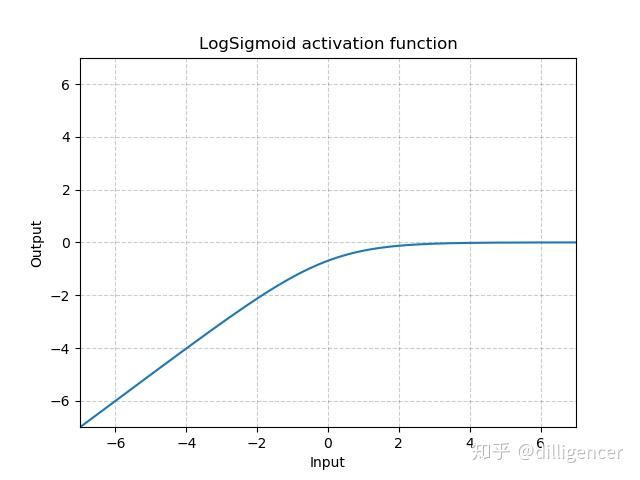
torch.nn.LogSigmoid

\[ LogSigmoid(x)=log(\frac{1}{1+exp(-x)}) \]

def LogSigmoid(x):
    return np.log(1/(np.exp(-x)+1))

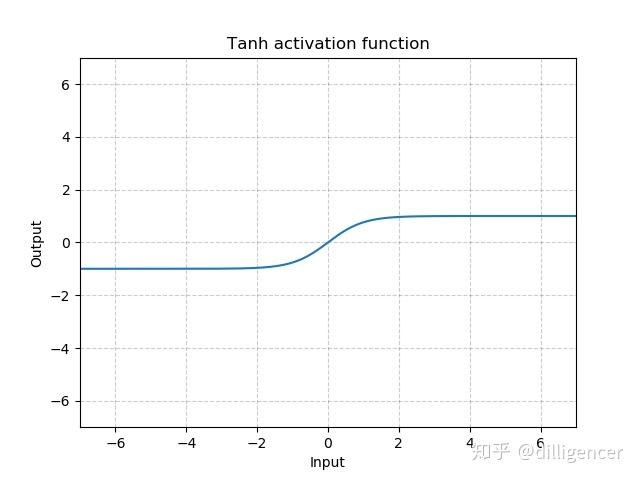
torch.nn.Tanh

\[ Tanh(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \]

def Tanh(x):
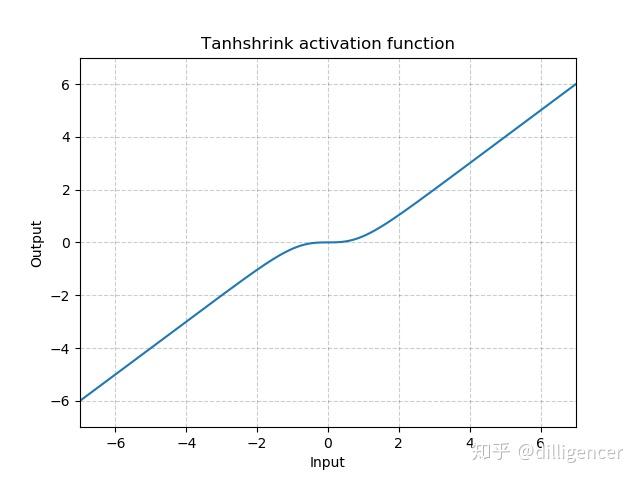
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))

torch.nn.Tanhshrink

\[ Tanhshrink(x)=x−Tanh(x) \]

def Tanhshrink(x):
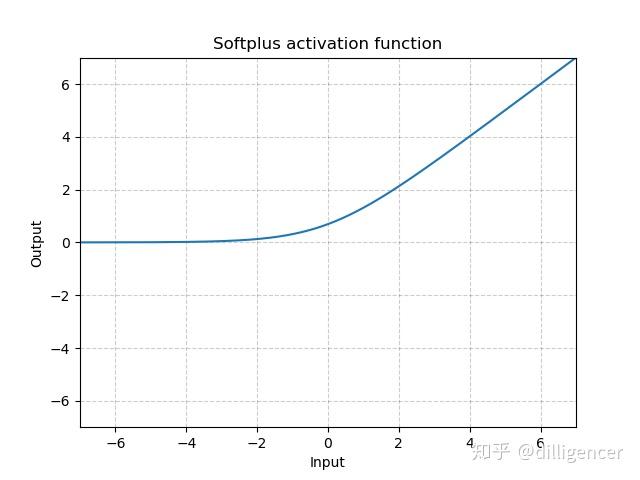
    return x-(np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))

torch.nn.Softplus(beta=1,threshold=20)

\[ Softplus(x)=\frac{1}{\beta}*log(1+exp(\beta*x)) \]

该函数可以看作是ReLu的平滑近似。

def Softplus(x,beta=1,threshold=20):
    return np.log(1+np.exp(beta*x))/beta

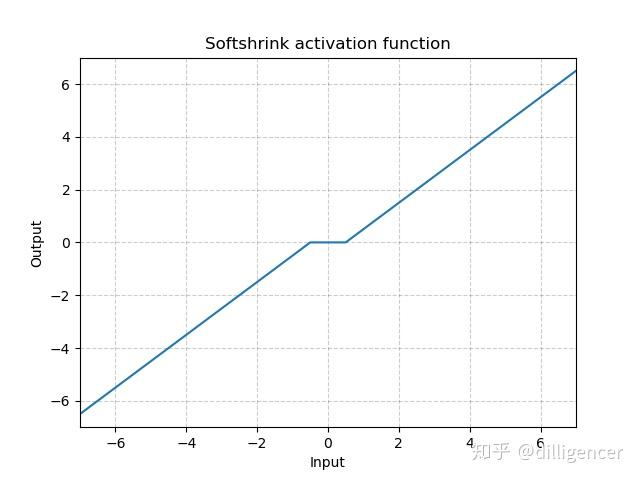
torch.nn.Softshrink(lambd=0.5)

\[ SoftShrinkage(x) = \left\{ \begin{array}{ll} x-\lambda, & \textrm{if $x>\lambda$}\\ x+\lambda, & \textrm{if $x<-\lambda$}\\ 0, & \textrm{otherwise} \end{array} \right. \]

λ的值默认设置为0.5

def Softshrink(x,lambd=0.5):
    if x>lambd:return x-lambd
    elif x<-lambd:return x+lambd
    else:return 0

参考资料

Pytorch激活函数及优缺点比较

PyTorch快速入门教程二（线性回归以及logistic回归）