《统计学习方法》阅读笔记——第2章-感知机
统计学习方法笔记——第2章-感知机
感知机(perceptron)是二分类的线性分类模型。其输入为实例的特征向量,输出为实例的类别,取+1 和–1 二值。
感知机模型:对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型;
感知机学习策略:基于误分类的损失函数;
感知机算法:利用梯度下降法对损失函数进行极小化(包括原始形式和对偶形式)。
感知机模型对线性可分的数据集比较有效。
数据集的线性可分性
给定一个数据集,如果存在某个超平面\(S\)能够将数据集的正、负实例点完全正确地划分到超平面两侧,即对所有\(y_i=+1\)的实例\(i\) ,有\(w·x+b>0\),对所有 \(y_i=-1\)的实例\(i\) ,有则称 数据集\(w·x+b<0\),则数据集是线性可分地(linearly separable data set);否则,称数据集线性不可分。
感知机模型
输入\(x\):输入空间(特征空间)\(\mathcal X \subseteq-\mathbf R^n\)中的点\(x \in \mathcal X\)。
输出\(y\):输出空间为\(\mathcal Y=\{+1,-1\}\),\(y\in \mathcal Y\)。
感知机:$f(x)=sign(w·x+b) \(,\)w$ 和\(b\) 为感知机模型参数,\(w\in \mathbf R^n\) 叫作权值(weight)或权值向量(weight vector),\(w\in \mathbf R\) 叫作偏置(bias),\(w·x\) 表示 \(w\) 和$ x \(的内积.\)sign$是符号函数,即: \[ \begin{align} sign= \left\{ \begin{array}{ll} +1, & \textrm{if $x \geq 0$}\\ -1, & \textrm{x<1} \end{array} \right. \end{align} \] 感知机模型的假设空间:定义在特征空间中的所有线性分类模型(linear classification model)或线性分类器(linear classifier),即函数集合\(\{ f| f (x) =w·x +b\}\)。
感知机模型的几何解释
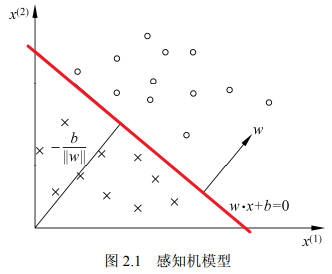
超平面:线性方程\(w·x+b=0\),对应于特征空间中的一个超平面,\(w\)为超平面法向量,\(b\) 是超平面的截距。如果特征空间是\(N\)维的,超平面就是\(N-1\)维的子空间。
分离超平面(separating hyperplane):一个超平面\(S\)将特征空间划分为两个部分,位于两部分的点(特征向量)分别被分为正、负两类。
特征空间维度为2的感知机模型如下图所示:
感知机学习策略
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。
为了确定感知机模型(超平面)参数 \(w , b\) ,需要确定一个学习策略,即定义(经验)损失函数并将损失函数极小化。
感知机学习的策略:在假设空间中选取使损失函数式最小的模型参数\(w, b\), 即感知机模型。
选择损失函数
方案1:误分类点的总数。但是,这样的损失函数不是参数 w , b 的连续可导函数,不易优化。
方案2(感知机采用):误分类点到超平面的总距离。
输入空间中任一点\(x_0\)到超平面 \(S\) 的距离: \[ \frac{1}{||w||}|w·x_0+b|,||w||是w的L_2范数 \] 对于误分类的数据\((x_i,y_i)\):\(-y_i(w·x_i+b)>0\)成立,对于一个正样本有\((w·x_i+b)>0\),预测错误则\(y_i=-1\),而对于一个负样本有\((w·x_i+b)<0\),预测错误则y_i=+1$。
因此,所有误分类点 \(x_i\) 到超平面 \(S\) 的总距离是: \[ -\frac{1}{||w||}\sum_{x_i\in M}y_i(w·x_i+b),M为误分类点集合 \] 由于\(\frac{1}{||w||}\)不影响正负号且算法结束时,整项都为0,不影响算法的最终结果,因此不考虑\(\frac{1}{||w||}\),就得到感知机的损失函数(对于给定数据集,为经验风险函数): \[ L(w,b)=-\sum_{x_i\in M}y_i(w·x_i+b) \] 一个特定的样本点的损失函数:在误分类时是参数 \(w , b\) 的线性函数,在正确分类时是 0。因此,给定训练数据集T ,损失函数 \(L (w,b)\)是 \(w, b\) 的连续可导函数。
感知机算法
感知机学习问题转化为求解损失函数式的最优化问题,最优化的方法是随机梯度下降法。感知机学习的具体算法,包括原始形式和对偶形式。
感知机学习算法的原始形式
给定一个训练数据集,求参数\(w,b\)使得损失函数最小: \[ \min_{w,b} L(w,b)=-\sum_{x_i\in M}y_i(w·x_i+b),M为误分类点集合 \] 感知机学习算法是误分类驱动的,具体采用随机梯度下降法(stochastic gradient descent)。每次随机选取一个误分类点使其梯度下降。


感知机学习算法由于采用不同的初值或选取不同的误分类点,解可以不同。
算法的收敛性
证明:对于线性可分数据集感知机学习算法原始形式收敛,即经过有限次迭代,可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。


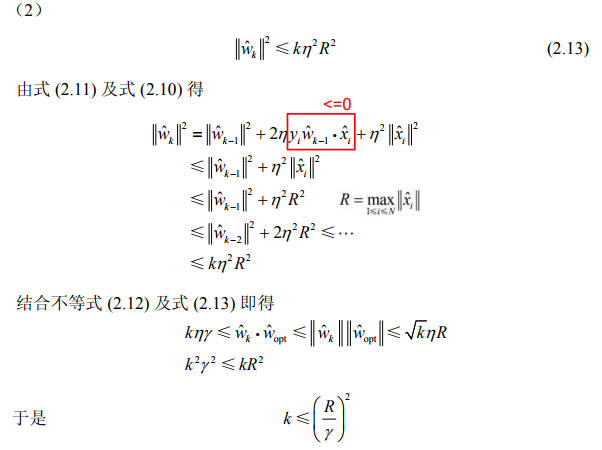
定理表明,误分类的次数 k 是有上界的,经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。也就是说,当训练数据集线性可分时,感知机学习算法原始形式迭代是收敛的。
感知机学习算法存在许多解,这些解既依赖于初值的选择,也依赖于迭代过程中误分类点的选择顺序。
为了得到唯一的超平面,需要对分离超平面增加约束条件。
当训练集线性不可分时,感知机学习算法不收敛,迭代结果会发生震荡。
感知机学习算法的对偶形式
对偶形式的基本想法是,将 \(w\) 和 \(b\) 表示为实例 \(x_i\) 和标记 \(y_i\)的线性组合的形式\(w=\sum_{i=1}^{N} \alpha_i y_i x_i,b=\sum_{i=1}^{N} \alpha_i y_i\),通过求解其系数而求得 \(w\) 和\(b\) 。

与原始形式一样,感知机学习算法的对偶形式迭代是收敛的(证明相同),存在多个解。
为什么要引出对偶形式?
参考资料:《浅析感知机(三)--收敛性证明与对偶形式以及python代码讲解》第一个评论。
进行随机梯度下降,选择一个样本xi,进行条件判断时,原始形式是需要做\(w\)和\(x_i\)的内积。这样每次条件判断时这个内积都得重新做一次,因为w每次迭代后都会更新。这样时间复杂度为O(n),n为特征维度。
将\(w\)写成\(x_i\)的线性组合后,\(w\)和\(x_i\)的内积可以转化为\(x_j,x_i\)的内积的线性组合形式,变化的是线性组合中的系数\(\alpha_j\),\(x_j,x_i\)的内积可以通过预先算好并存表。每次条件判断时只需查表并做线性求和即可。对于\(x_i\)来说,\(x_i,x_j\)的组合共有N个,N表示训练集大小,因此共需查表求和N次,时间复杂度为O(N)。
当n明显大于N时,对偶形式可以减少计算时间。
习题
主要参考资料:
DataWhale资料-第2章 感知机 (datawhalechina.github.io)
习题2.1
题目
Minsky 与 Papert 指出:感知机因为是线性模型,所以不能表示复杂的函数,如异或 (XOR)。验证感知机为什么不能表示异或。
证明
异或函数(XOR)
| a | b | y=a⊕b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
假设\(x\)向量只有两个维度\(x_1,x_2\),有以下四个样本:
| 样本 | x1 | x2 | y |
|---|---|---|---|
| 0 | 0 | 0 | -1 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | -1 |
图例法
在二维坐标系上可视化样本,从下图可以看出,无法使用一条直线完全将两类样本分开,所以异或问题是线性不可分的。
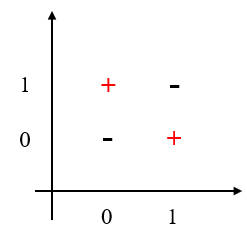
反证法
假设感知机模型可以表示异或问题,带入上述四个样本点,逐步求\(w1,w2和b\):
- 根据\(x_1=0, x_2=0, y=-1\),则\(w \cdot x +b < 0\),可得\(b < 0\);
- 根据\(x_1=0, x_2=1, y=1\),则\(w_2 + b > 0\),结合\(b < 0\),可得\(w_2 > -b > 0\);
- 根据\(x_1=1, x_2=0, y=1\),则\(w_1 + b > 0\),结合\(b < 0\),可得\(w_1 > -b > 0\);
- 根据\(x_1=1, x_2=1\),并结合\(w_1 + b > 0、w_2 > 0\),则\(w_1 + w_2 + b > 0\),可得\(y=1\),与异或条件中的\(y=-1\)矛盾。
所以假设不成立,原命题成立,即感知机模型不能表示异或。
sklearn感知机代码验证
使用sklearn的Perceptron类构建感知机模型,从模型的参数上观察,感知机模型的参数:w= [0. 0.] b= 0.0,无法表示异或。
from sklearn.linear_model import Perceptron |
习题2.2
题目
模仿例题 2.1,构建从训练数据求解感知机模型的例子。
解
训练集需要线性可分,使用鸢尾花的前100个数据样本:
from sklearn.datasets import load_iris |
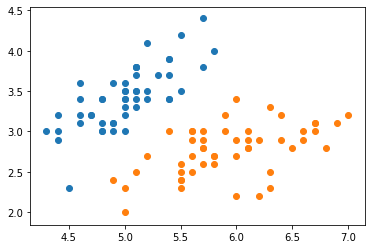
sklearn.linear_model.Perceptron实现
from sklearn.linear_model import Perceptron |
可视化结果如下:
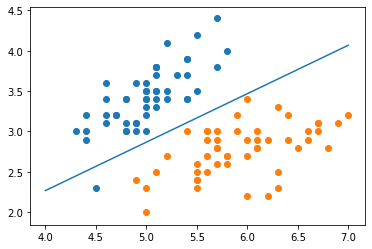
numpy实现
回顾一下算法的原始形式:

import numpy as np |
model = Perceptron(X, y) |
可视化结果如下:

习题2.3
题目
证明以下定理:样本集线性可分的充分必要条件是正实例点所构成的凸壳与负实例点所构成的凸壳互不相交。
证明
凸壳定义:
设集合\(S \subset R^n\),是由\(R^n\)中的\(k\)个点所组成的集合,即\(S=\{x_1,x_2,\cdots, x_k\}\)。定义\(S\)的凸壳\(\text{conv}(S)\)为: \[ \text{conv}(S) = \left\{ x = \sum_{i=1}^k \lambda_i x_i \Big| \sum_{i=1}^k \lambda_i=1,\lambda_i \geqslant 0, i=1,2,\cdots, k \right\} \]
线性可分
给定一个数据集,如果存在某个超平面\(S\)能够将数据集的正、负实例点完全正确地划分到超平面两侧,即对所有\(y_i=+1\)的实例\(i\) ,有\(w·x+b>0\),对所有 \(y_i=-1\)的实例\(i\) ,有则称 数据集\(w·x+b<0\),则数据集是线性可分地(linearly separable data set);否则,称数据集线性不可分。
必要性:线性可分->凸壳互不相交
反证法:
假设原命题不成立,即:样本集线性可分,正实例点所构成的凸壳与负实例点所构成的凸壳相交。
设数据集\(T\)中的正例点集为\(S_+\),\(S_+\)的凸壳为\(\text{conv}(S_+)\),负实例点集为\(S_-\),\(S_-\)的凸壳为\(\text{conv}(S_-)\)。
假设样本集线性可分,正实例点所构成的凸壳与负实例点所构成的凸壳相交,即存在某个元素\(s\),同时满足\(s \in \text{conv}(S_+)\)和\(s \in \text{conv}(S_-)\)。
充分性:凸壳互不相交->线性可分
证明思路:
- 根据凸壳不相交,找到一个超平面;
- 证明这个超平面可将两个互不相交的凸壳分隔开(反证法),即存在一个超平面分隔两类样本,则样本集满足线性可分。
证明步骤:
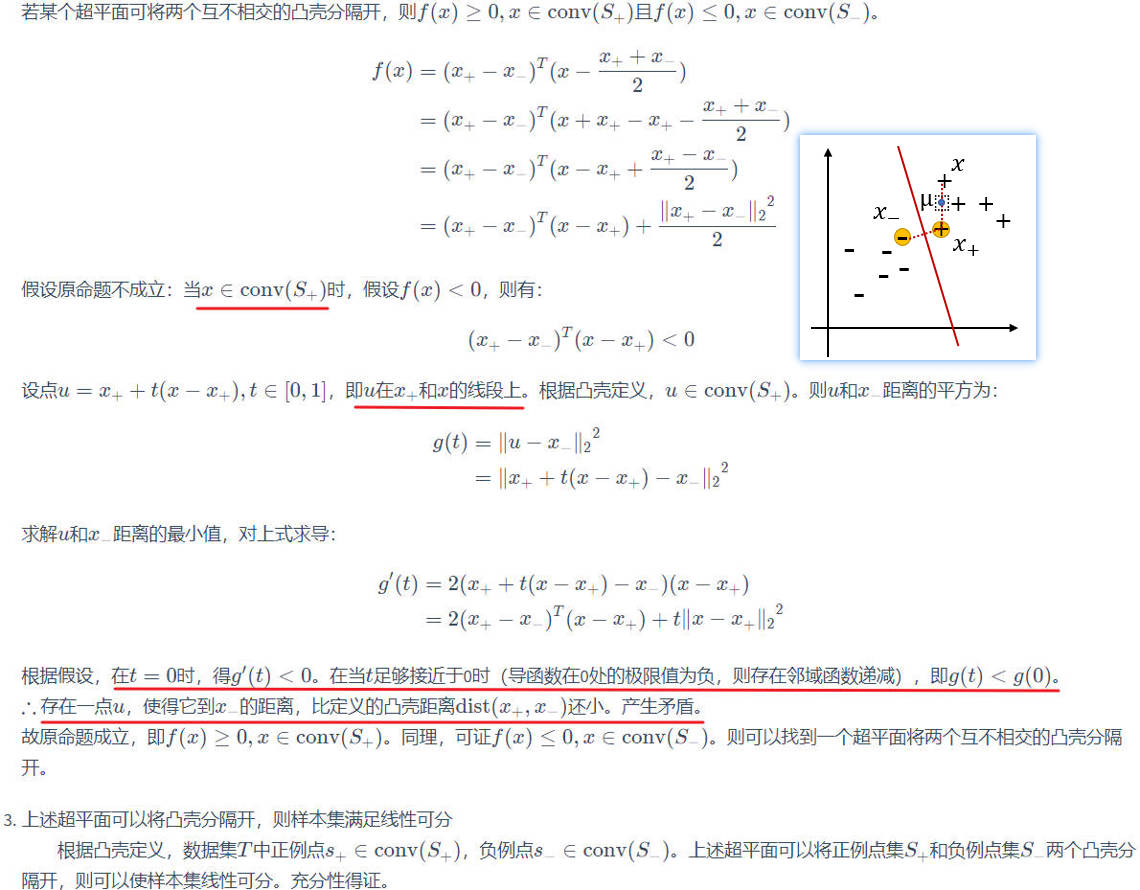
根据凸壳不相交,找到一个超平面:可以根据两个凸壳最近样本(\(x_+\in S_+,x_-\in S_-\))的连线作为法线,过法线中点的超平面作为分割超平面,当维度为2维时,示意图如下图所示:

定义\(dist(x_+,x_-)\)为两个凸壳集合中点距离的最小值。定义以\((x_+, x_-)\)为法线,且过两点中点的超平面为\(f(x|w,b)=0\),则参数为: \[ \begin{align} f(x∣w,b)&=(x_+−x_−)^T(x−\frac{x_++x_−}{2})\\ w&=(x_+−x_−)^T, \\b&=−\frac{1}{2}(||x_+||_2^2−||x_−||_2^2) \end{align} \]
证明这个超平面可将两个互不相交的凸壳分隔开(反证法),即存在一个超平面分隔两类样本,则样本集满足线性可分: