《统计学习方法》阅读笔记——第3章-k近邻法

统计学习方法笔记——第3章-k近邻法

k 近邻法（k-nearest neighbor，k-NN）是一种基本分类与回归方法。《统计学习方法》一书中讨论分类问题中的 k 近邻法。

k 近邻算法

用k 近邻法分类时，对新的实例，根据给定的距离度量，找出其 k 个最近邻的训练实例，根据最邻近 k 个实例的类别，通过多数表决等方式对该实例的类别进行预测（这 k 个实例的多数属于某个类，就把该输入实例分为这个类）。

有以下特点：

1. k 近邻法不具有显式的学习过程。
2. k 近邻法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。
3. k值的选择、距离度量及分类决策规则是k 近邻法的三个基本要素。当训练集、距离度量、 k 值及分类决策规则确定后，k临近法的结果唯一确定。

特别的，当$ k=1\(时，称为**最近邻算法**：对于输入的实例点（特征向量）\) x$ ，最近邻法将训练数据集中与$ x \(最邻近点的类作为\) x$ 的类。

k 近邻模型

模型

k 近邻法使用的模型实际上是对特征空间的划分。

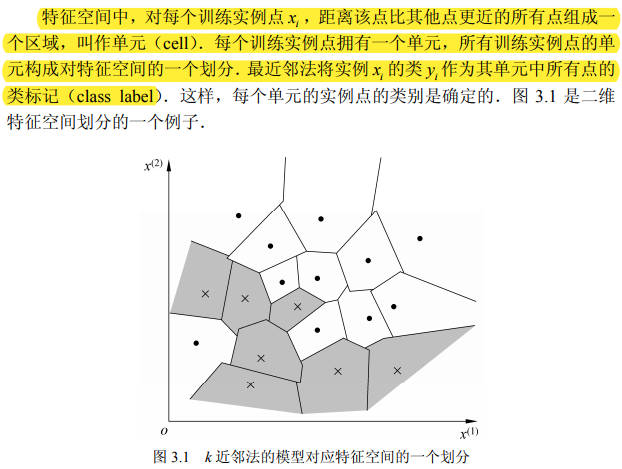
模型由三个基本要素：距离度量、 k 值的选择和分类决策规则决定。

距离度量

距离度量特征空间两个实例点的相似程度。

关于距离度量可以参考之前的笔记：距离计算

由不同的距离度量所确定的最近邻点是不同的。

k 值的选择

k 值的选择会对 k 近邻法的结果产生重大影响。

1. 选择较小的 k 值：
   • 相当于用较小的邻域中的训练实例进行预测；
   • “学习”的近似误差（approximation error）会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用；
   • 缺点是“学习”的估计误差（estimation error）会增大，预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错；
   • k 值的减小就意味着整体模型变得复杂，容易发生过拟合。
2. 选择较大的 k 值：
   • 相当于用较大邻域中的训练实例进行预测；
   • 其优点是可以减少学习的估计误差；
   • 缺点是学习的近似误差会增大，这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误；
   • k 值的增大就意味着整体的模型变得简单(当k=N时，无论输入实例是什么都预测其属于训练实例中最多的类)。

在应用中，k 值一般取一个比较小的数值。通常采用交叉验证法来选取最优的 k 值。

分类决策规则

k 近邻法中的分类决策规则往往是多数表决，即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。

多数表决规则等价于经验风险最小化，证明如下：

经验风险最小化->误分类率最小：误分类概率为：\(P(Y\neq f(x))=1-P(Y=f(x))\)。

对于给定的实例 \(x\in \mathcal X\)，其最近邻的 \(k\) 个训练实例点构成集合\(N_k(x)\) ．如果涵盖\(N_k(x)\)的区域的类别是\(c_j\)，那么误分类率是： \[ \frac{1}{k}\sum_{x_i \in N_k(x)}I(y_i\neq c_j)=1-\frac{1}{k}\sum_{x_i \in N_k(x)}I(y_i= c_j) \] 于是要最大化\(\sum_{x_i \in N_k(x)}I(y_i= c_j)\)，等同于多数表决规则。

k 近邻法的实现：kd 树

实现 k 近邻法时，搜索k近邻的最简单的实现方法是线性扫描（linear scan），计算输入实例与每一个训练实例的距离。当训练集很大时，计算非常耗时，这种方法是不可行的。

kd 树是二叉树，利用一种特殊的结构存储训练数据，以减少计算距离的次数，从而对训练数据进行快速 k 近邻搜索。

构造kd树

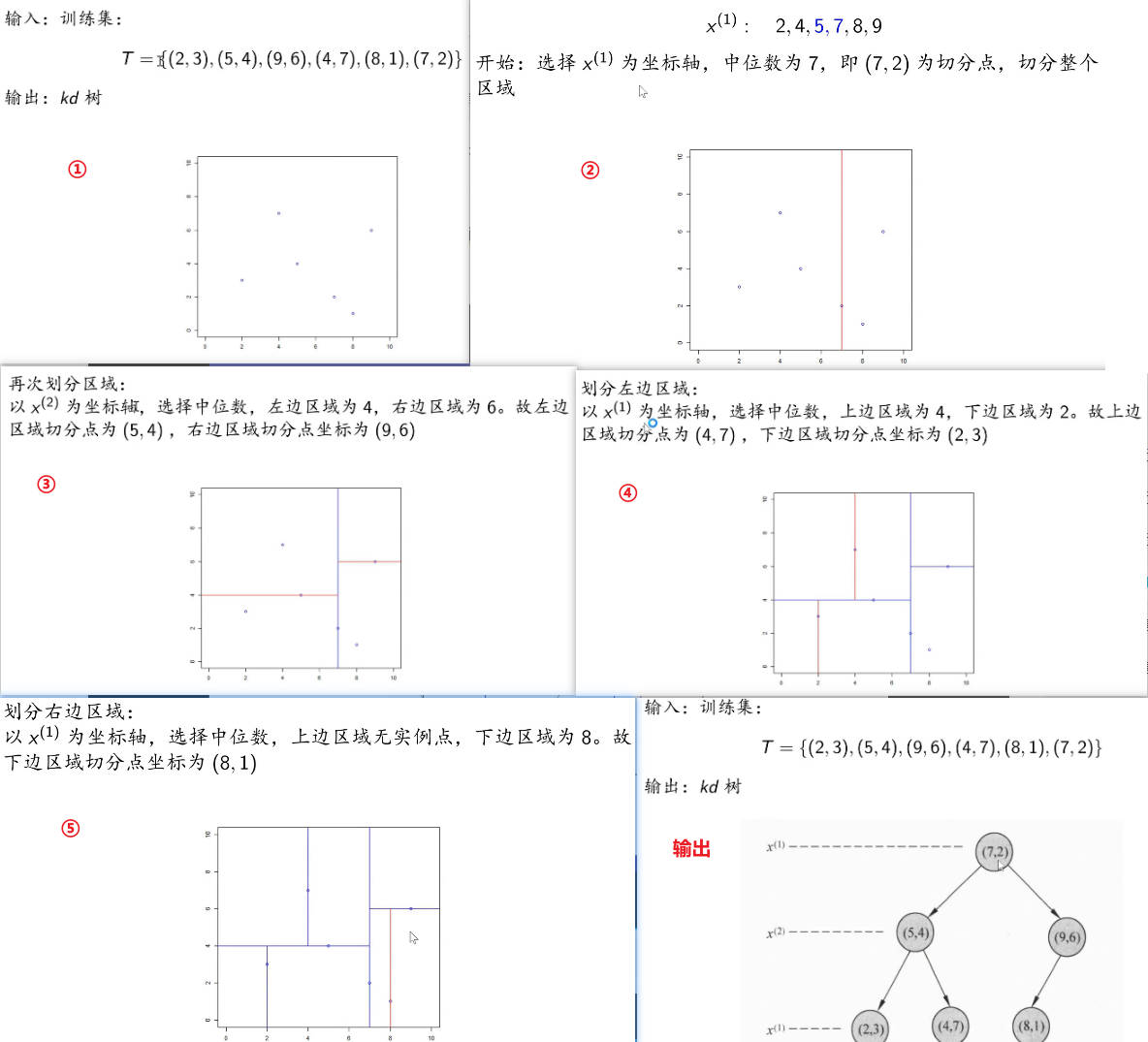
kd 树是二叉树，表示对k 维空间（注意此处的k与k近邻法的k意义不同）的一个划分（partition）。不断地用垂直于坐标轴的超平面将k 维空间切分，构成一系列的k 维超矩形区域，从而构建kd树。kd 树的每个结点对应于一个 k 维超矩形区域。

构造kd树算法

构造kd树案例

搜索kd树

如果实例点是随机分布的，kd 树搜索的平均计算复杂度是\(O (\log N)\) ， \(N\)是训练实例数。

kd 树更适用于训练实例数远大于空间维数(\(N>>k\))时的 k 近邻搜索。当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描。

用kd树的最邻近搜索

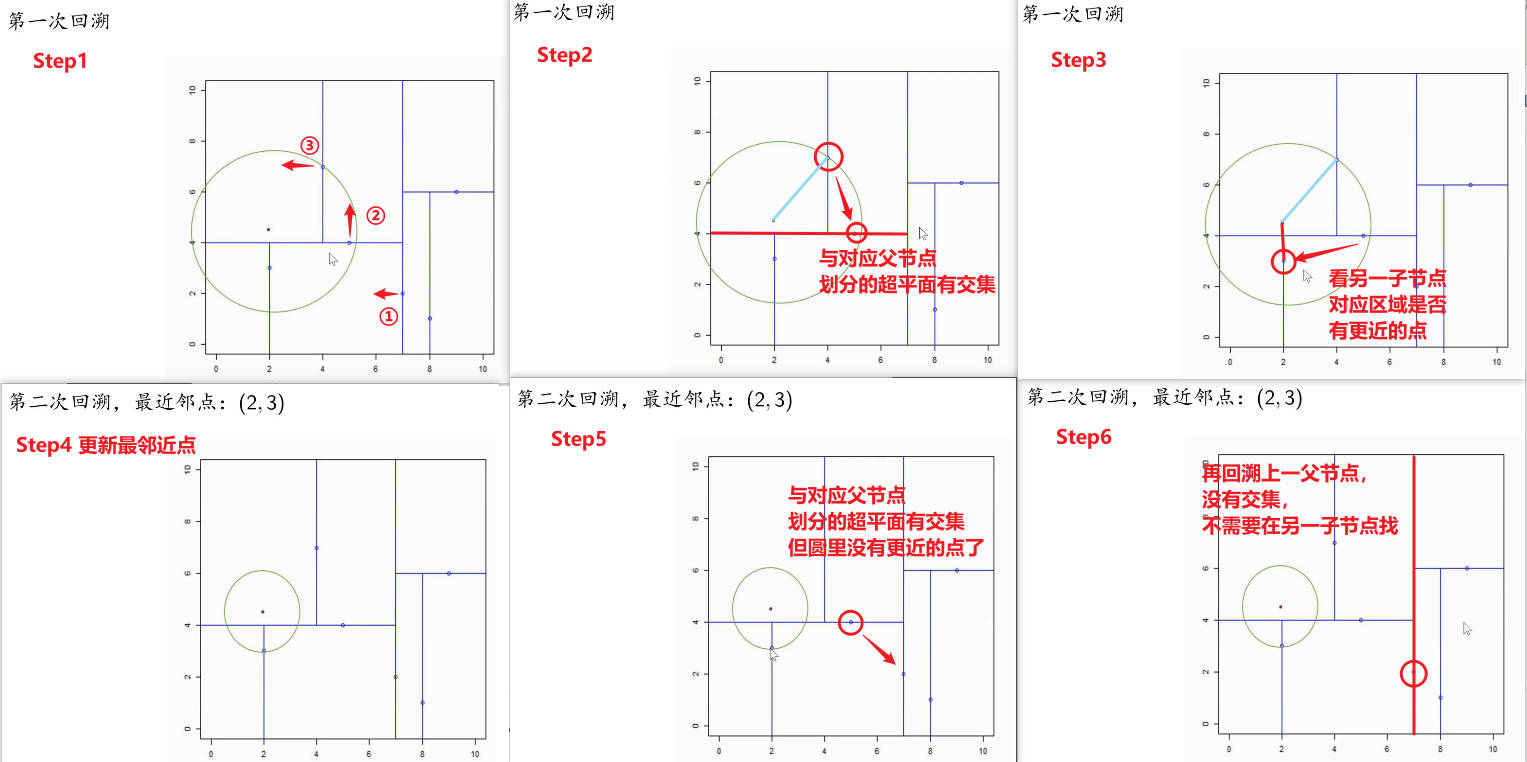
最近邻搜索案例(kd树)

以前面构造的kd树为例，对点\((2,4.5)\)的最近邻搜索过程。

习题

习题3.1

题目

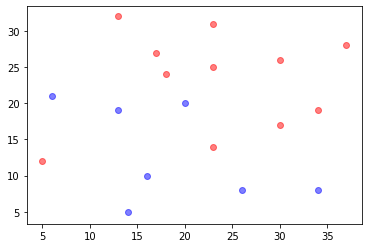
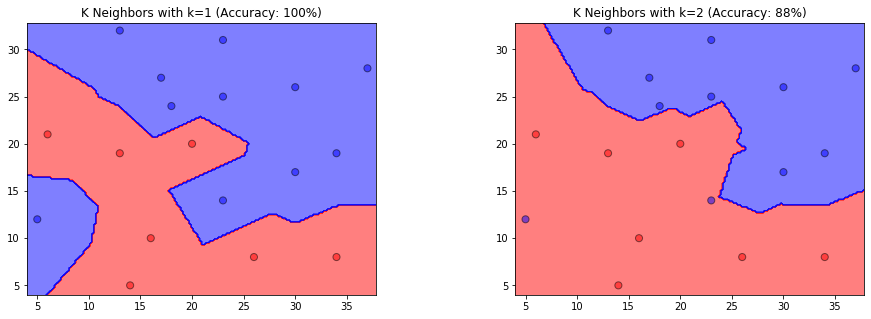
参照图 3.1，在二维空间中给出实例点，画出k 为 1 和 2 时的k 近邻法构成的空间划分，并对其进行比较，体会k 值选择与模型复杂度及预测准确率的关系。

解

训练集

import numpy as np
import matplotlib.pyplot as plt
data = np.array([[5, 12, 1],
                 [6, 21, 0],
                 [14, 5, 0],
                 [16, 10, 0],
                 [13, 19, 0],
                 [13, 32, 1],
                 [17, 27, 1],
                 [18, 24, 1],
                 [20, 20, 0],
                 [23, 14, 1],
                 [23, 25, 1],
                 [23, 31, 1],
                 [26, 8, 0],
                 [30, 17, 1],
                 [30, 26, 1],
                 [34, 8, 0],
                 [34, 19, 1],
                 [37, 28, 1]])
# 得到特征向量
X_train = data[:, 0:2]
# 得到类别向量
y_train = data[:, 2]
#可视化数据集
indexes=y_train==1
plt.scatter(X_train[indexes,0:1],X_train[indexes,1:2],label='1',color='red',alpha=0.5)
plt.scatter(X_train[~indexes,0:1],X_train[~indexes,1:2],label='0',color='blue',alpha=0.5)

创建并训练模型

利用sklearn.neighbors.KNeighborsClassifier，分别设置k=1和k=2，得到两个k近邻分类器，默认为欧氏距离，参数设置可参考sklearn.neighbors.KNeighborsClassifier()函数解析（最清晰的解释）_种树最好的时间是10年前，其次是现在！！！-CSDN博客：

from matplotlib.colors import ListedColormap
from sklearn.neighbors import KNeighborsClassifier
#（1）使用已给的实例点，采用sklearn的KNeighborsClassifier分类器，
# 对k=1和2时的模型进行训练
# 分别构造k=1和k=2的k近邻模型
models = (KNeighborsClassifier(n_neighbors=1, n_jobs=-1),
          KNeighborsClassifier(n_neighbors=2, n_jobs=-1))
# 模型训练
models = (clf.fit(X_train, y_train) for clf in models)

可视化结果

# 设置图形标题
titles = ('K Neighbors with k=1',
          'K Neighbors with k=2')

# 设置图形的大小和图间距
fig = plt.figure(figsize=(15, 5))
plt.subplots_adjust(wspace=0.4, hspace=0.4)

# 分别获取第1个和第2个特征向量
X0, X1 = X_train[:, 0], X_train[:, 1]

# 得到坐标轴的最小值和最大值
x_min, x_max = X0.min() - 1, X0.max() + 1
y_min, y_max = X1.min() - 1, X1.max() + 1

# 构造网格点坐标矩阵
# 设置0.2的目的是生成更多的网格点，数值越小，划分空间之间的分隔线越清晰
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.2),
                     np.arange(y_min, y_max, 0.2))

for clf, title, ax in zip(models, titles, fig.subplots(1, 2).flatten()):
    # （2）使用matplotlib的contourf和scatter，画出k为1和2时的k近邻法构成的空间划分
    # 对所有网格点进行预测
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # 设置颜色列表
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    # 根据类别数生成颜色
    cmap = ListedColormap(colors[:len(np.unique(Z))])
    # 绘制分隔线，contourf函数用于绘制等高线，alpha表示颜色的透明度，一般设置成0.5
    ax.contourf(xx, yy, Z, cmap=cmap, alpha=0.5)

    # 绘制样本点
    ax.scatter(X0, X1, c=y_train, s=50, edgecolors='k', cmap=cmap, alpha=0.5)

    # （3）根据模型得到的预测结果，计算预测准确率，并设置图形标题
    # 计算预测准确率
    acc = clf.score(X_train, y_train)
    # 设置标题
    ax.set_title(title + ' (Accuracy: %d%%)' % (acc * 100))

plt.show()

分析结果

1. 当\(k=1\)时，训练集的分类精度为100%，当\(k=2\)时，训练集的分类精度为88%。
2. k 值过小整体模型变得复杂，容易发生过拟合。

习题3.2

题目

利用例题 3.2 构造的 kd 树求点 \(x =(3,4.5)^T\) 的最近邻点。

解

方法1：图解

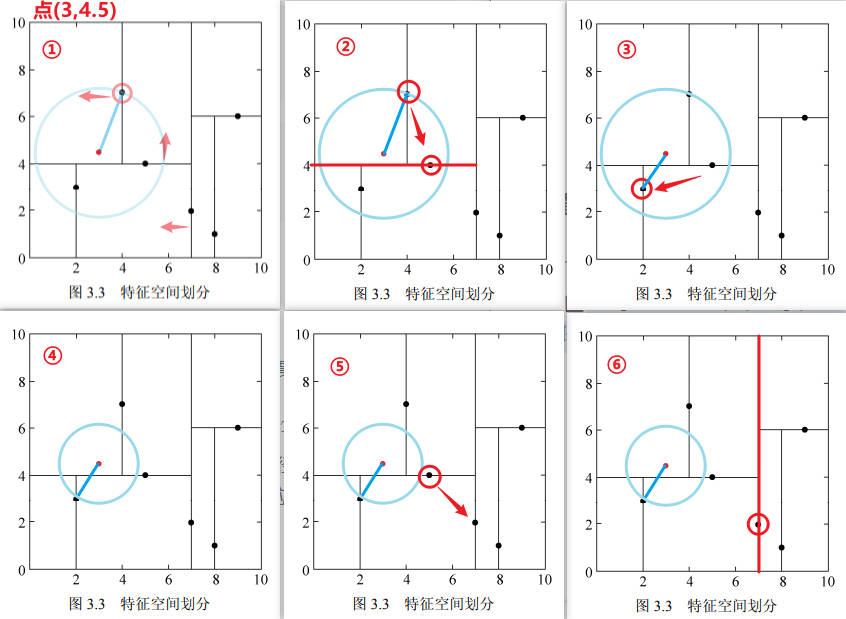
根据以上图解可知， \(x =(3,4.5)^T\) 的最近邻点是\((2,3)^T\)。

方法2：sklearn代码解

import numpy as np
from sklearn.neighbors import KDTree

# 构造例题3.2的数据集
train_data = np.array([[2, 3],
                       [5, 4],
                       [9, 6],
                       [4, 7],
                       [8, 1],
                       [7, 2]])
# （1）使用sklearn的KDTree类，构建平衡kd树
# 设置leaf_size为2，表示平衡树
tree = KDTree(train_data, leaf_size=2)

# （2）使用tree.query方法，设置k=1，查找(3, 4.5)的最近邻点
# dist表示与最近邻点的距离，ind表示最近邻点在train_data的位置
dist, ind = tree.query(np.array([[3, 4.5]]), k=1)
node_index = ind[0]

# （3）得到最近邻点
x1 = train_data[node_index][0][0]
x2 = train_data[node_index][0][1]
print("x点(3,4.5)的最近邻点是({0}, {1})".format(x1, x2))

#x点(3,4.5)的最近邻点是(2, 3)

习题3.3

题目

参照算法 3.3，写出输出为 \(x\) 的 k 近邻的算法

解

算法回顾(算法3.3)

输入：已构造的kd树；目标点\(x\)； 输出：\(x\)的k近邻

1. 在kd树中找出包含目标点\(x\)的叶结点：从根结点出发，递归地向下访问树。若目标点\(x\)当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止；
2. 如果“当前k近邻点集”元素数量小于k或者叶节点距离小于“当前k近邻点集”中最远点距离，那么将叶节点插入“当前k近邻点集”；
3. 递归地向上回退，在每个结点进行以下操作：
   • 如果“当前k近邻点集”元素数量小于k或者当前节点距离小于“当前k近邻点集”中最远点距离，那么将该节点插入“当前k近邻点集”。
   • 检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前k近邻点集”中最远点间的距离为半径的超球体相交。
     • 如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着，递归地进行近邻搜索；
     • 如果不相交，向上回退；
4. 当回退到根结点时，搜索结束，最后的“当前k近邻点集”即为\(x\)的近邻点。

构造平衡kd树

方法1：

from sklearn.neighbors import KDTree
tree = KDTree(train_data, leaf_size=2)
# ind：最近的3个邻居的索引
# dist：距离最近的3个邻居
X = train_data[0].reshape(1,-1)
dist, ind = tree.query(X, k=5)

print ('ind:',ind)
print ('dist:',dist)
#ind: [[0 1 3 5 4]]
#dist: [[0.         3.16227766 4.47213595 5.09901951 6.32455532]]

方法2：

import json
class Node:
    """节点类"""

    def __init__(self, value, index, left_child, right_child):
        self.value = value.tolist()
        self.index = index
        self.left_child = left_child
        self.right_child = right_child

    def __repr__(self):
        return json.dumps(self, indent=3, default=lambda obj: obj.__dict__, ensure_ascii=False, allow_nan=False)

class KDTree:
    """kd tree类"""

    def __init__(self, data):
        # 数据集
        self.data = np.asarray(data)
        # kd树
        self.kd_tree = None
        # 创建平衡kd树
        self._create_kd_tree(data)

    def _split_sub_tree(self, data, depth=0):
        # 算法3.2第3步：直到子区域没有实例存在时停止
        if len(data) == 0:
            return None
        # 算法3.2第2步：选择切分坐标轴, 从0开始（书中是从1开始）j(mod k)+1
        l = depth % data.shape[1]
        # 对数据进行排序
        data = data[data[:, l].argsort()]
        # 算法3.2第1步：将所有实例坐标的中位数作为切分点
        median_index = data.shape[0] // 2
        # 获取结点在数据集中的位置
        node_index = [i for i, v in enumerate(
            self.data) if list(v) == list(data[median_index])]
        return Node(
            # 本结点
            value=data[median_index],
            # 本结点在数据集中的位置
            index=node_index[0],
            # 左子结点
            left_child=self._split_sub_tree(data[:median_index], depth + 1),
            # 右子结点
            right_child=self._split_sub_tree(
                data[median_index + 1:], depth + 1)
        )

    def _create_kd_tree(self, X):
        self.kd_tree = self._split_sub_tree(X)

    def query(self, data, k=1):
        data = np.asarray(data)
        hits = self._search(data, self.kd_tree, k=k, k_neighbor_sets=list())
        dd = np.array([hit[0] for hit in hits])
        ii = np.array([hit[1] for hit in hits])
        return dd, ii

    def __repr__(self):
        return str(self.kd_tree)

    @staticmethod
    def _cal_node_distance(node1, node2):
        """计算两个结点之间的距离，欧氏距离"""
        return np.sqrt(np.sum(np.square(node1 - node2)))

    def _search(self, point, tree=None, k=1, k_neighbor_sets=None, depth=0):
        if k_neighbor_sets is None:
            k_neighbor_sets = []
        if tree is None:
            return k_neighbor_sets
        # (1)找到包含目标点x的叶结点
        if tree.left_child is None and tree.right_child is None:
            # 更新当前k近邻点集
            return self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)

        if point[0][depth % k] < tree.value[depth % k]:
            direct = 'left'
            next_branch = tree.left_child
        else:
            direct = 'right'
            next_branch = tree.right_child
        #递归地向下访问kd树
        k_neighbor_sets=self._search(point, tree=next_branch, k=k, depth=depth + 1, k_neighbor_sets=k_neighbor_sets)
        print(k_neighbor_sets,depth)
        # (3)(a) 判断当前结点，并更新当前k近邻点集
        k_neighbor_sets = self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)
        print(k_neighbor_sets)
        # (3)(b)检查另一子结点对应的区域是否相交，注意判断另一子结点是否存在
        if direct == 'left' and tree.right_child:
            if len(k_neighbor_sets) < k: #如果没有找到足够个数的邻居直接更新
                return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,k_neighbor_sets=k_neighbor_sets)
            else:#否则的话更新更近的邻居
                node_distance = self._cal_node_distance(point, tree.right_child.value)
                if k_neighbor_sets[0][0] > node_distance:
                # 如果相交，递归地进行近邻搜索
                    return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,k_neighbor_sets=k_neighbor_sets)
        elif direct == 'right' and tree.left_child:
            if len(k_neighbor_sets) < k:#如果没有找到足够个数的邻居直接更新
                return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,k_neighbor_sets=k_neighbor_sets)
            else:#否则的话更新更近的邻居
                node_distance = self._cal_node_distance(point, tree.left_child.value)
                if k_neighbor_sets[0][0] > node_distance:
                    return self._search(point, tree=tree.left_child, k=k, depth=depth + 1, k_neighbor_sets=k_neighbor_sets)
        
        return k_neighbor_sets

    def _update_k_neighbor_sets(self, best, k, tree, point):
        # 计算目标点与当前结点的距离
        node_distance = self._cal_node_distance(point, tree.value)
        if len(best) == 0:
            best.append((node_distance, tree.index, tree.value))
        elif len(best) < k:
            # 如果“当前k近邻点集”元素数量小于k
            self._insert_k_neighbor_sets(best, tree, node_distance)
        else:
            # 叶节点距离小于“当前 𝑘 近邻点集”中最远点距离
            if best[0][0] > node_distance:
                best = best[1:]
                self._insert_k_neighbor_sets(best, tree, node_distance)
        return best

    @staticmethod
    def _insert_k_neighbor_sets(best, tree, node_distance):
        """将距离最远的结点排在前面"""
        n = len(best)
        for i, item in enumerate(best):
            if item[0] < node_distance:
                # 将距离最远的结点插入到前面
                best.insert(i, (node_distance, tree.index, tree.value))
                break
        if len(best) == n:
            best.append((node_distance, tree.index, tree.value))

打印邻近节点

# 打印信息
def print_k_neighbor_sets(k, ii, dd):
    if k == 1:
        text = "x点的最近邻点是"
    else:
        text = "x点的%d个近邻点是" % k

    for i, index in enumerate(ii):
        res = X_train[index]
        if i == 0:
            text += str(tuple(res))
        else:
            text += ", " + str(tuple(res))

    if k == 1:
        text += "，距离是"
    else:
        text += "，距离分别是"
    for i, dist in enumerate(dd):
        if i == 0:
            text += "%.4f" % dist
        else:
            text += ", %.4f" % dist

    print(text)

查询k近邻

import numpy as np

X_train = np.array([[2, 3],
                    [5, 4],
                    [9, 6],
                    [4, 7],
                    [8, 1],
                    [7, 2]])
tree = KDTree(train_data)
# ind：最近的3个邻居的索引
# dist：距离最近的3个邻居
X = train_data[0].reshape(1,-1)
dist, ind = tree.query(X, k=5)

print ('ind:',ind)
print ('dist:',dist)
#ind: [4 5 3 1 0]
#dist: [6.32455532 5.09901951 4.47213595 3.16227766 0.        ]

参考资料

李航 统计学习方法 第2版

DataWhale资料-第3章 k近邻法 (datawhalechina.github.io)

sklearn.neighbors.KNeighborsClassifier()函数解析（最清晰的解释）_种树最好的时间是10年前，其次是现在！！！-CSDN博客

【合集】十分钟 机器学习 系列视频 《统计学习方法》