统计学习方法笔记——第6章-逻辑斯谛回归与最大熵模型
逻辑斯谛回归模型logistic regression
虽然叫回归模型但是是经典的分类方法 之一,属于对数线性模型。
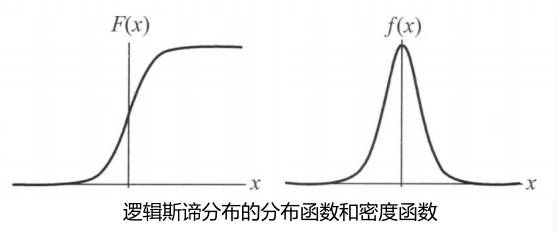
逻辑斯谛分布logistic distribution
设\(X\) 是连续随机变量,\(X\) 服从逻辑斯谛分布是指\(X\) 具有下列分布函数和密度函数: \[
\begin{align}F(x)=P(X\leq x)=\frac{1}{1+e^{-(x-\mu)/\gamma}}\\
f(x)=F'(x)=\frac{e^{-(x-\mu)/\gamma} }{\gamma(1+e^{-(x-\mu)/\gamma})^2}
\end{align}
\] 式中,\(\mu\) 为位置参数,\(\gamma>0\) 为形状参数。图形如下图所示,分布哈数曲线以点\((\mu,\frac{1}{2})\) 为中心对称,曲线在中心附近增长速度较快,在两端增长速度较慢。形状参数7的值越小,曲线在中心附近增长得越快。
二项逻辑斯谛回归模型
二分类模型,为如下的条件概率分布,通过监督学习的方法来估计模型参数\(w,b\) ,将\(x\) 分到概率值较大的一类。 \[
\begin{align}P(Y=1|x)=\frac{e^{(w·x+b)}}{1+e^{(w·x+b)}}\\
P(Y=0|x)=\frac{1}{1+e^{(w·x+b)}}
\end{align}
\] 一个事件的几率(odds)是指该事件发生的概率\(p\) 与该事件不发生的概率\(1-p\) 的比值。该事件的几率是\(\frac{p}{1-p}\) ,该事件的对数几率(log odds)或logit函数是: \[
logit(p)=\log \frac{p}{1-p}
\] 将\(p=P(Y=1|x)\) 带入上式(这里将\(w\) 重新定义为了\((w,b)^T\) ),得到: \[
\log\frac{P(Y=1|x)}{1-P(Y=1|x)}=w·x
\] 在逻辑斯谛回归模型中,输出\(Y = 1\) 的对数几率是输入\(x\) 的线性函数。
模型参数估计-极大似然法
多项逻辑斯谛回归
多分类模型,为如下条件概率分布: \[
\begin{align}P(Y=k|x)&=\frac{e^{(w_k·x)}}{1+\sum_{k=1}^{K-1}e^{(w_k·x)}},k=1,2,3...K-1\\
P(Y=K|x)&=\frac{1}{1+\sum_{k=1}^{K-1}e^{(w_k·x)}}
\end{align}
\]
最大熵模型
最大熵模型(maximum entropy model)由最大熵原理推导实现。
最大熵原理
最大熵原理是指在满足约束条件的模型集合中选取熵最大的模型。 最大熵原理是选择最优模型的一个准则 ,是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型 。
随机变量\(X\) 的概率分布是\(P(x)\) ,其熵为: \[
H(P)=-\sum_xP(x)\log P(x)
\] 在满足约束条件下,没有更多信息时,不确定的部分都是”等可能的“。因此,最大熵原理通过熵的最大化来表示等可能性 。(\(P(x)=\frac{1}{|X|}\) ,即,\(X\) 服从均匀分布时,熵最大。)
最大熵模型定义
首先考虑模型\(P(Y|X)\) 的约束条件,如果模型能够获取训练数据中的信息,那么就可以假设下面两个期望值相等: \[
E_P(f)=E_{\tilde P}(f)
\] 其中,\(E_P(f)\) 表示特征函数\(f(x,y)\) 关于模型\(\tilde P(Y|X)\) 与经验分布\(\tilde P(X)\) 的期望值,\(E_{\tilde P}(f)\) 表示特征函数\(f(x,y)\) 关于模型\(\tilde P(X,Y)\) 的期望值。
具体来说,\(E_P(f)\) 和\(E_{\tilde P}(f)\) 由以下表达式计算: \[
\begin{align}
E_P(f)=&\sum_{x,y}\tilde P(x,y)f(x,y)
\\E_{\tilde P}(f)=&\sum_{x,y}\tilde P(x)P(y|x)f(x,y)
\\其中,f(x,y)为特征函数,f(x,y)=& \left\{ \begin{array}{ll}
1 & \textrm{x与y满足某一事实}\\
0 & \textrm{否则}
\end{array} \right.
\end{align}
\] 给定数据集,联合分布\(P(X,Y)\) 和边缘分布\(P(X)\) 的经验分布用\(\tilde P(X,Y)\) 、\(\tilde P(X)\) 表示。 \[
\begin{align}
\tilde P(X=x,Y=y)&=\frac{\mathcal v(X=x,Y=y)}{N}
\\
\tilde P(X=x)&=\frac{\mathcal v(X=x)}{N}
\end{align}
\] \(v(X=x,Y=y)\) 为训练集中\((x,y)\) 出现的频数,\(v(X=x)\) 表示训练数据中\(x\) 出现的频数,\(N\) 为训练样本容量。
因此得到约束条件: \[
\sum_{x,y}\tilde P(x,y)f(x,y)=\sum_{x,y}\tilde P(x)P(y|x)f(x,y)
\] 如果有\(n\) 个特征函数,那么就有\(n\) 个约束条件。
最大熵模型定义如下:
最大熵模型的学习策略
最大熵模型的学习等价于约束最优化问题。
引入拉格朗日乘子将原始约束最优化问题转化为无约束的最优化对偶问题。 通过求解对偶问题求解原始问题。
推导如下:
可得最大熵模型是由下面两个式子表示的条件概率分布: \[
\begin{align}
P_w(y|x)=&\frac{1}{Z_w(x)}exp(\sum_{i=1}^nw_if_i(x,y))\\
其中,Z_w(X)为规范化因子,Z_w=&\sum_y exp(\sum_{i=1}^{n}w_if_i(x,y))
\end{align}
\]
最大熵模型的极大似然估计
对偶函数的极大化等价于最大熵模型的极大似然估计。
证明如下:
模型学习的最优化算法
逻辑斯谛回归模型、最大熵模型学习归结为以似然函数为目标函数的最优化问题 ,通常通过迭代算法求解。
常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。
梯度下降算法
算法原理
选取适当的初值不断迭代,更新\(x\) 的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数值下降最快的方向,在迭代的每一步,以负梯度方向更新\(x\) 的值, 从而达到减少函数值的目的。
算法流程
改进的迭代尺度法
改进的迭代尺度法(improved iterative scaling, IIS)是一种最大熵模型学习的最优化算法。
算法原理
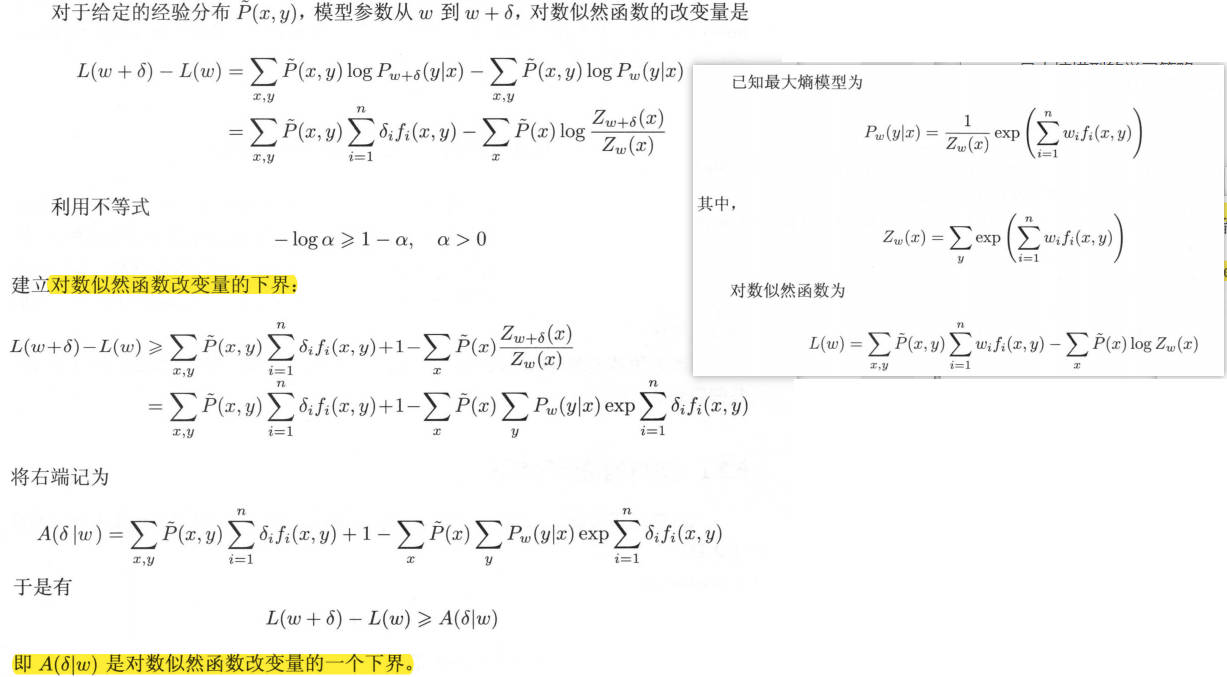
希望找到一个新的参数向量\(w + \delta=(w_1 + \delta_1, w_2+\delta_2,…,w_n + \delta_n)^T\) 使得模型的对数似然函数值增大。如果能有这样一种参数向量更新的方法\(\tau\) :\(w\rightarrow w+\delta\) 那么就可以重复使用这一方法,直至找到对数似然函数的最大值。
所以目标为求解\(\delta\) ,求解\(\delta\) 的公式推导如下:
算法流程
关键步骤是(2)(a),求解\(\delta_i\) ,具体的,如果\(f^\#(x,y)\) 为常数,可以直接求解,否则可以通过牛顿法,利用数值计算进行求解:
牛顿法
求解无约束最优化问题的常用方法 之一,有收敛速度快的优点,是一种迭代算法 ,每一步需要求解目标函数的海赛矩阵的逆矩阵 ,计算比较复杂。
算法原理
算法流程
核心是求解\(p_k\) ,因而需要求海赛矩阵的逆,计算复杂,拟牛顿法是用一个矩阵近似代替海赛矩阵的逆或海塞矩阵来优化求解的。
拟牛顿法
算法原理
拟牛顿法用一个 \(n\) 阶矩阵\(G_k=G(x^{(k)})\) 来近似代替\(H_k^{-1}=H^{-1}(x^{(k)})\) 。
牛顿法中,海赛矩阵需要满足以下关系:
拟牛顿法要求矩阵\(G_k\) 满足同样的条件:
有多种方法实现\(G_{k+1}=G_k+\Delta G_k\) 的计算:包括DFP算法、BFGS算法等等。
DFP(Davidon-Fletcher-Powell)算法
DFP 算法选择\(G_{k+1}\) 的方法是,假设每一步迭代中矩阵\(G_{k+1}\) 是由\(G_{k}\) 加上两个附加项构成的。
DFP(Davidon-Fletcher-Powell)算法流程
BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法
BFGS方法考虑用\(B_k\) 逼近海赛矩阵\(H\) .
BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法流程
习题
主要参考第6章 Logistic回归与最大熵模型
习题6.1
题目
确认Logistic分布属于指数分布族。
解
指数分布族
对于随机变量\(x\) ,在给定参数\(\theta\) 下,其概率密度函数满足如下形式称之为指数分布族: $$ \[\begin{align}
f(x|\theta)=h(x)\exp(\theta^T\cdot T(x)-A(\theta))
\\
其中,\left\{ \begin{array}{ll}
\theta为自然参数,可以为向量形式,\\
T(\theta)为充分统计量,\\
A(\theta)为累计函数,作用是确保概率和为1,\\
h(x)为底层观测值
\end{array} \right.
\end{align}\] $$ 逻辑斯谛回归是广义线性模型的一种,广义线性模型与最大熵模型都源于指数分布族。
以二项逻辑斯谛回归模型为例证明其属于指数分布族。
二项逻辑斯谛回归模型属于指数分布族的证明
二项逻辑斯谛回归模型可表示为: \[
\begin{align}P(Y=1|x)=\frac{e^{(w·x)}}{1+e^{(w·x)}}\\
P(Y=0|x)=\frac{1}{1+e^{(w·x)}}
\end{align}
\] 可转化为: \[
\begin{align}
P(y|x)=&[\frac{e^{(w·x)}}{1+e^{(w·x)}}]^y[\frac{1}{1+e^{(w·x)}}]^{(1-y)}
\\
=&\exp[y\log(\frac{e^{(w·x)}}{1+e^{(w·x)}})+(1-y)\log(\frac{1}{1+e^{(w·x)}})]
\end{align}
\] 令\(\pi(x)=1+e^{(w·x)}\) ,则有: \[
\begin{align}
P(y|x)=&\exp[(y\log(\frac{\pi(x)}{\pi(x)+1}))+(1-y)\log \frac{1}{1+\pi(x)}]\\
=&\exp(y\log \pi(x)-\log(\pi(x)+1))
\end{align}
\] 那么令: \[
\begin{align}
\left\{ \begin{array}{ll}
\theta=\log(\pi(x))(注意),\\
T(\theta)=y(注意),\\
A(\theta)=log(\pi(x)+1) ,\\
h(\theta)=1,\\
\end{array} \right.
\end{align}
\] 可证二项逻辑斯谛回归模型属于指数分布族。
习题6.2
题目
写出Logistic回归模型学习的梯度下降算法。
解
梯度下降算法
Logistic回归模型的梯度下降算法
对于Logistic回归模型的目标函数(对数似然函数): \[
L(w)=∑_{i=1}^N[y_i(w⋅x_i)−\log(1+\exp(w⋅x_i))]
\] 梯度函数: \[
\nabla L(w)=\left[\frac{\partial L(w)}{\partial w^{(0)}}, \cdots, \frac{\partial L(w)}{\partial w^{(n)}}\right]
\] 其中,对数似然函数求偏导: \[
\frac{\partial L(w)}{\partial w^{(k)}}=\sum_{i=1}^N\left[x_i \cdot y_i-\frac{\exp (w^{(k)} \cdot x_i) \cdot x_i}{1+\exp (w^{(k)} \cdot x_i)}\right]
\] 因此Logistic回归模型的梯度下降算法:
""" 逻辑斯蒂回归算法实现(牛顿法,拟牛顿法,梯度下降法)-调用sklearn模块 """ from sklearn.linear_model import LogisticRegressionimport numpy as npX_train=np.array([[3 ,3 ,3 ],[4 ,3 ,2 ],[2 ,1 ,2 ],[1 ,1 ,1 ],[-1 ,0 ,1 ],[2 ,-2 ,1 ]]) y_train=np.array([1 ,1 ,1 ,0 ,0 ,0 ]) methodes=["liblinear" ,"newton-cg" ,"lbfgs" ,"sag" ,"saga" ] res=[] X_new = np.array([[1 , 2 , -2 ]]) for method in methodes: clf=LogisticRegression(solver=method,intercept_scaling=2 ,max_iter=1000 ) clf.fit(X_train,y_train) y_predict=clf.predict(X_new) X_test=X_train y_test=y_train correct_rate=clf.score(X_test,y_test) res.append((y_predict,correct_rate)) methodes=["liblinear" ,"newton-cg" ,"lbfgs " ,"sag " ,"saga " ] print ("solver选择: {}" .format (" " .join(method for method in methodes)))print ("{}被分类为: {}" .format (X_new[0 ]," " .join(str (re[0 ]) for re in res)))print ("测试{}组数据,正确率: {}" .format (X_train.shape[0 ]," " .join(str (round (re[1 ],1 )) for re in res)))
sklearn.linear_model.LogisticRegression参数设置
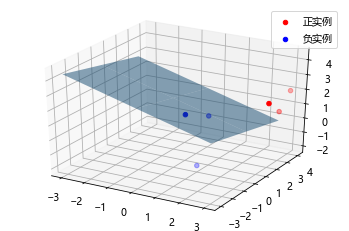
自编程实现Logistic回归模型学习的梯度下降法 from scipy.optimize import fminboundfrom pylab import mplimport numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dmpl.rcParams['font.sans-serif' ] = ['Microsoft YaHei' ] class MyLogisticRegression : def __init__ (self, max_iter=10000 , distance=3 , epsilon=1e-6 ): """ Logistic回归 :param max_iter: 最大迭代次数 :param distance: 一维搜索的长度范围 :param epsilon: 迭代停止阈值 """ self.max_iter = max_iter self.epsilon = epsilon self.w = None self.distance = distance self._X = None self._y = None @staticmethod def preprocessing (X ): """将原始X末尾加上一列,该列数值全部为1""" row = X.shape[0 ] y = np.ones(row).reshape(row, 1 ) return np.hstack((X, y)) @staticmethod def sigmod (x ): return 1 / (1 + np.exp(-x)) def grad (self, w ): z = np.dot(self._X, w.T) grad = self._X * (self._y - self.sigmod(z)) grad = grad.sum (axis=0 ) return grad def like_func (self, w ): z = np.dot(self._X, w.T) f = self._y * z - np.log(1 + np.exp(z)) return np.sum (f) def fit (self, data_x, data_y ): self._X = self.preprocessing(data_x) self._y = data_y.T w = np.array([[0 ] * self._X.shape[1 ]], dtype=np.float ) k = 0 fw = self.like_func(w) for _ in range (self.max_iter): grad = self.grad(w) if (np.linalg.norm(grad, axis=0 , keepdims=True ) < self.epsilon).all (): self.w = w break def f (x ): z = w - np.dot(x, grad) return -self.like_func(z) _lambda = fminbound(f, -self.distance, self.distance) w1 = w - np.dot(_lambda , grad) fw1 = self.like_func(w1) if np.linalg.norm(fw1 - fw) < self.epsilon or \ (np.linalg.norm((w1 - w), axis=0 , keepdims=True ) < self.epsilon).all (): self.w = w1 break k += 1 w, fw = w1, fw1 self.grad_ = grad self.n_iter_ = k self.coef_ = self.w[0 ][:-1 ] self.intercept_ = self.w[0 ][-1 ] def predict (self, x ): p = self.sigmod(np.dot(self.preprocessing(x), self.w.T)) p[np.where(p > 0.5 )] = 1 p[np.where(p < 0.5 )] = 0 return p def score (self, X, y ): y_c = self.predict(X) error_rate = np.sum (np.abs (y_c - y.T)) / y_c.shape[0 ] return 1 - error_rate def draw (self, X, y ): y = y[0 ] X_po = X[np.where(y == 1 )] X_ne = X[np.where(y == 0 )] ax = plt.axes(projection='3d' ) x_1 = X_po[0 , :] y_1 = X_po[1 , :] z_1 = X_po[2 , :] x_2 = X_ne[0 , :] y_2 = X_ne[1 , :] z_2 = X_ne[2 , :] ax.scatter(x_1, y_1, z_1, c="r" , label="正实例" ) ax.scatter(x_2, y_2, z_2, c="b" , label="负实例" ) ax.legend(loc='best' ) x = np.linspace(-3 , 3 , 3 ) y = np.linspace(-3 , 3 , 3 ) x_3, y_3 = np.meshgrid(x, y) a, b, c, d = self.w[0 ] z_3 = -(a * x_3 + b * y_3 + d) / c ax.plot_surface(x_3, y_3, z_3, alpha=0.5 ) plt.show()
数据
X_train = np.array([[3 , 3 , 3 ], [4 , 3 , 2 ], [2 , 1 , 2 ], [1 , 1 , 1 ], [-1 , 0 , 1 ], [2 , -2 , 1 ]]) y_train = np.array([[1 , 1 , 1 , 0 , 0 , 0 ]]) clf = MyLogisticRegression(epsilon=1e-6 ) clf.fit(X_train, y_train) clf.draw(X_train, y_train) print ("迭代次数:{}次" .format (clf.n_iter_))print ("梯度:{}" .format (clf.grad_))print ("权重:{}" .format (clf.w[0 ]))print ("模型准确率:%0.2f%%" % (clf.score(X_train, y_train) * 100 ))
习题6.3
题目
写出最大熵模型学习的DFP算法。(关于一般的DFP算法参见附录B)。
解
一般的DFP算法
最大熵模型: \[
\begin{align}
P_w(y|x)=&\frac{1}{Z_w(x)}exp(\sum_{i=1}^nw_if_i(x,y))\\
其中,Z_w(X)为规范化因子,Z_w=&\sum_y exp(\sum_{i=1}^{n}w_if_i(x,y))
\end{align}
\] 目标函数: \[
\begin{align}
\min_{w∈R^n}f(w)=∑_x \tilde P(x)\log y∑\exp \big(∑_{i=1}^nw_if_i(x,y) \big)−∑_{x,y}\tilde P(x,y)∑_{i=1}^nw_if_i(x,y)
\end{align}
\] 梯度: \[
g(w) = \left( \frac{\partial f(w)}{\partial w_1}, \frac{\partial f(w)}{\partial w_2}, \cdots, \frac{\partial f(w)}{\partial w_n}\right)^T
\] 其中 \[
\frac{\partial f(w)}{\partial w_1} = \sum \limits_{x,y} \tilde{P}(x) P_w(y|x) f_i(x,y) - E_{\tilde{P}}(f_i), \quad i=1,2,\cdots,n
\] 最大熵模型学习的DFP算法:
自编程实现最大熵模型学习的DFP算法 import copyfrom collections import defaultdictimport numpy as npfrom scipy.optimize import fminboundclass MaxEntDFP : def __init__ (self, epsilon, max_iter=1000 , distance=0.01 ): """ 最大熵的DFP算法 :param epsilon: 迭代停止阈值 :param max_iter: 最大迭代次数 :param distance: 一维搜索的长度范围 """ self.distance = distance self.epsilon = epsilon self.max_iter = max_iter self.w = None self._dataset_X = None self._dataset_y = None self._y = set () self._xyID = {} self._IDxy = {} self._pxy_dic = defaultdict(int ) self._N = 0 self._n = 0 self.n_iter_ = 0 def init_params (self, X, y ): self._dataset_X = copy.deepcopy(X) self._dataset_y = copy.deepcopy(y) self._N = X.shape[0 ] for i in range (self._N): xi, yi = X[i], y[i] self._y.add(yi) for _x in xi: self._pxy_dic[(_x, yi)] += 1 self._n = len (self._pxy_dic) self.w = np.zeros(self._n) for i, xy in enumerate (self._pxy_dic): self._pxy_dic[xy] /= self._N self._xyID[xy] = i self._IDxy[i] = xy def calc_zw (self, X, w ): """书中第100页公式6.23,计算Zw(x)""" zw = 0.0 for y in self._y: zw += self.calc_ewf(X, y, w) return zw def calc_ewf (self, X, y, w ): """书中第100页公式6.22,计算分子""" sum_wf = self.calc_wf(X, y, w) return np.exp(sum_wf) def calc_wf (self, X, y, w ): sum_wf = 0.0 for x in X: if (x, y) in self._pxy_dic: sum_wf += w[self._xyID[(x, y)]] return sum_wf def calc_pw_yx (self, X, y, w ): """计算Pw(y|x)""" return self.calc_ewf(X, y, w) / self.calc_zw(X, w) def calc_f (self, w ): """计算f(w)""" fw = 0.0 for i in range (self._n): x, y = self._IDxy[i] for dataset_X in self._dataset_X: if x not in dataset_X: continue fw += np.log(self.calc_zw(x, w)) - \ self._pxy_dic[(x, y)] * self.calc_wf(dataset_X, y, w) return fw def fit (self, X, y ): self.init_params(X, y) def calc_dfw (i, w ): """计算书中第107页的拟牛顿法f(w)的偏导""" def calc_ewp (i, w ): """计算偏导左边的公式""" ep = 0.0 x, y = self._IDxy[i] for dataset_X in self._dataset_X: if x not in dataset_X: continue ep += self.calc_pw_yx(dataset_X, y, w) / self._N return ep def calc_ep (i ): """计算关于经验分布P(x,y)的期望值""" (x, y) = self._IDxy[i] return self._pxy_dic[(x, y)] return calc_ewp(i, w) - calc_ep(i) def calc_gw (w ): return np.array([[calc_dfw(i, w) for i in range (self._n)]]).T Gk = np.array(np.eye(len (self.w), dtype=float )) w = self.w gk = calc_gw(w) if np.linalg.norm(gk, ord =2 ) < self.epsilon: self.w = w return k = 0 for _ in range (self.max_iter): pk = -Gk.dot(gk) def _f (x ): z = w + np.dot(x, pk).T[0 ] return self.calc_f(z) _lambda = fminbound(_f, -self.distance, self.distance) delta_k = _lambda * pk w += delta_k.T[0 ] gk1 = calc_gw(w) if np.linalg.norm(gk1, ord =2 ) < self.epsilon: self.w = w break yk = gk1 - gk Pk = delta_k.dot(delta_k.T) / (delta_k.T.dot(yk)) Qk = Gk.dot(yk).dot(yk.T).dot(Gk) / (yk.T.dot(Gk).dot(yk)) * (-1 ) Gk = Gk + Pk + Qk gk = gk1 k += 1 self.w = w self.n_iter_ = k def predict (self, x ): result = {} for y in self._y: prob = self.calc_pw_yx(x, y, self.w) result[y] = prob return result
数据
dataset = np.array([['no' , 'sunny' , 'hot' , 'high' , 'FALSE' ], ['no' , 'sunny' , 'hot' , 'high' , 'TRUE' ], ['yes' , 'overcast' , 'hot' , 'high' , 'FALSE' ], ['yes' , 'rainy' , 'mild' , 'high' , 'FALSE' ], ['yes' , 'rainy' , 'cool' , 'normal' , 'FALSE' ], ['no' , 'rainy' , 'cool' , 'normal' , 'TRUE' ], ['yes' , 'overcast' , 'cool' , 'normal' , 'TRUE' ], ['no' , 'sunny' , 'mild' , 'high' , 'FALSE' ], ['yes' , 'sunny' , 'cool' , 'normal' , 'FALSE' ], ['yes' , 'rainy' , 'mild' , 'normal' , 'FALSE' ], ['yes' , 'sunny' , 'mild' , 'normal' , 'TRUE' ], ['yes' , 'overcast' , 'mild' , 'high' , 'TRUE' ], ['yes' , 'overcast' , 'hot' , 'normal' , 'FALSE' ], ['no' , 'rainy' , 'mild' , 'high' , 'TRUE' ]]) X_train = dataset[:, 1 :] y_train = dataset[:, 0 ] mae = MaxEntDFP(epsilon=1e-4 , max_iter=1000 , distance=0.01 ) mae.fit(X_train, y_train) print ("模型训练迭代次数:{}次" .format (mae.n_iter_))print ("模型权重:{}" .format (mae.w))result = mae.predict(['overcast' , 'mild' , 'high' , 'FALSE' ]) print ("预测结果:" , result)
参考资料
Datawhale资料-第6章 Logistic回归与最大熵模型 (datawhalechina.github.io)
李航 统计学习方法 第2版
李航《统计学习方法》第2版 第6章课后习题答案






















 最大熵模型学习的DFP算法
最大熵模型学习的DFP算法