西瓜书阅读笔记——第2章-模型评估与选择(到2.3.2)
西瓜书阅读笔记——第2章-模型评估与选择(到2.3.2)
记录和补充一些比较容易混淆、易忘、容易表述错误、以及方便取用的内容。
经验误差与过拟合
经验误差
误差error:学习器实际预测输出与样本真实输出之间的差异;
训练误差training error/经验误差empirical error:学习器在训练集上的误差;
泛化误差generalization error:在新样本上的误差。
过拟合、欠拟合
过拟合:在训练集上表现很好(过于好),但在测试集或者新样本上表现很差(泛化性很差),把在训练集中包含的不太一般的特性学到了(这些特性在整体样本空间中没有或者没那么重要,比如说训练集的噪声);
欠拟合:在训练集上就表现很差,模型学习能力低下。
模型评估与选择
对候选模型的泛化误差进行评估,选择泛化误差最小的模型。我们无法直接获得全部的样本空间,因此泛化误差是无法准确计算的,所以我们根据已有的数据集构建测试集来估计泛化误差。
留出法hold-out
获得的所有样本数据)划分为两个互斥的集合,将其中一个作为训练集S,另一个作为验证集T,即D=SUT,S∩T=Φ。在S上训练出模型后,再用T来评估其测试误差,作为泛化误差的估计值;
训练集/验证集的划分要尽可能保持数据分布的一致性,尽量减少因数据划分过程引入额外的偏差而对最终结果产生的影响,例如在分类任务中,通过分层抽样(stratified sampling)保持S与T内的样本各个类别的比例和原分布相似;
单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
训练集与验证集间的比例就不能过于随便,通常情况下我们将2/3到4/5的样本划分出来用于训练。
一般而言,测试集至少应含30个样例。(《机器学习》——周志华p26)
代码
基于留出法的原理,利用sklearn的train_test_split函数进行数据集划分,该函数的参数及返回值如下:
X:待分割的样本集中的自变量部分,通常为二维数组或矩阵的形式;
y:待分割的样本集中的因变量部分,通常为一维数组;
test_size:用于指定验证集所占的比例,有以下几种输入类型:
1.float型,0.0~1.0之间,此时传入的参数即作为验证集的比例;
2.int型,此时传入的参数的绝对值即作为验证集样本的数量;
3.None,这时需要另一个参数train_size有输入才生效,此时验证集去为train_size指定的比例或数量的补集;
4.缺省时为0.25,但要注意只有在train_size和test_size都不输入值时缺省值才会生效;
train_size:基本同test_size,但缺省值为None,其实test_size和train_size输入一个即可;
random_state:int型,控制随机数种子,默认为None,即纯随机(伪随机);
stratify:控制分类问题中的分层抽样,默认为None,即不进行分层抽样,当传入为数组时,则依据该数组进行分层抽样(一般传入因变量所在列);
shuffle:bool型,用来控制是否在分割数据前打乱原数据集的顺序,默认为True,分层抽样时即stratify为None时该参数必须传入False;
返回值:
依次返回训练集自变量、测试集自变量、训练集因变量、测试集因变量,因此使用该函数赋值需在等号右边采取X_train, X_test, y_train, y_test'的形式。
案例代码:
from sklearn import datasets
import pandas as pd
'''载入数据'''
X,y = datasets.load_iris(return_X_y=True)
'''采取分层抽样时的数据集分割'''
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,stratify=y)
'''打印各个数据集的形状'''
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
'''打印训练集中因变量的各类别数目情况'''
print(pd.value_counts(y_train))
'''打印验证集集中因变量的各类别数目情况'''
print(pd.value_counts(y_test))
交叉验证法cross validation
先将数据集D划分为k个大小相似的互斥子集,即\(D=D_1UD_2U...UD_k,D_i∩D_j=\phi(i≠j)\),每个子集Di都尽可能保持数据分布的一致性(从D中通过分层采样)。然后每次用k-1个子集的并集作为训练集,剩下的一个子集作为验证集;这样就可获得k组的训练+验证集,从而可以进行k次训练与测试,最终返回的是这k个测试结果的均值。交叉验证法的稳定性和保真性在很大程度上取决与k的取值,因此交叉验证法又称作“k折交叉验证”(k-fold cross validation),k最常见的取值为10,即“10折交叉验证”,其他常见的有5,20等。
代码
利用sklearn的KFold函数划分数据集:
KFold():以生成器的方式产出每一次交叉验证所需的训练集与验证集,其主要参数如下:
n_splits:int型,控制k折交叉中的k,默认是3;
shuffle:bool型,控制是否在采样前打乱原数据顺序;
random_state:设置随机数种子,默认为None,即不固定随机水平;
案例代码:
import numpy as np
X = np.random.randint(1,10,20)
kf = KFold(n_splits=5)
for train,test in kf.split(X):
print(train,'\n',test)
留一法Leave-one-out LOO
留一法是交叉验证法的一个特例,假定数据集D中包含m个样本,令k=m,每个子集包含一个样本。显然,留一法不受随机样本划分方式的影响,因为m个样本只有唯一的方式划分m个子集,留一法使用的训练集与初始数据集相比只少了一个样本,这就使得在绝大多数情况下,留一法中被实际评估的模型与期望评估的用D训练出的模型很相似,因此,留一法的评估结果往往被认为比较准确,但其也有一个很大的缺陷:当数据集比较大时,训练m个模型的计算成本非常大。
优点
评估结果往往被认为比较准确。
缺点
计算成本非常大。
代码
利用sklearn的LeaveOneOut函数划分数据集:
LeaveOneOut():对应先前所介绍的留出法中的特例,留一法,因为其性质很固定,所以无参数需要调节。
案例代码:
import numpy as np
X = np.random.randint(1,10,5)
kf = LeaveOneOut()
for train,test in kf.split(X):
print(train,'\n',test)
LeavePOut():是留一法的一个变种,唯一的不同就是每次留出p个而不是1个样本作为验证集,唯一的参数是p。
利用sklearn的LeavePOut函数划分数据集:
案例代码:
import numpy as np
X = np.random.randint(1,10,5)
kf = LeavePOut(p=2)
for train,test in kf.split(X):
print(train,'\n',test)
自助法bootstrapping
每次随机从D中挑选一个样本,将其拷贝放入D‘,然后再将该样本放回初始数据集D中,使得样本在下次采样时仍然有可能被采集到,循环执行m遍,就得到了m个样本的数据集D’。
优点
自助法在数据集较小、难以有效划分训练/测试集时很有用;此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大的好处。
缺点
自助法产生的数据集改变了初始数据集的分布,这会引入估计偏差。
代码(来源:机器学习之数据集划分-自助法(bootstrapping))
# 随机产生我们的数据集
x = np.random.randint(-10, 10, 10) # 前两个参数表示范围,第三个参数表示个数
index = [i for i in range(len(x))] # 数据集的下标
train_set = [] # 训练集
train_index = [] # 用于记录训练集各个元素的下标
test_set = [] # 测试集
test_index = [] # 用于记录测试集各个元素的下标
# 进行m次放回抽样
for i in range(len(x)):
train_index.append(np.floor(np.random.random()*len(x)))
# 计算D\D'
test_index = list(set(index).difference(set(train_index)))
# 取数,产生训练/测试集
for i in range(len(train_index)):
train_set.append(x[int(train_index[i])]) # 这里记得强制转换为int型,否则会报错
for i in range(len(test_index)):
test_set.append(x[int(test_index[i])])
# 打印结果进行验证
print("data set: ", x)
print("train set: ", train_set)
print("test set: ", test_set)
顺序约束采样
对于具有强顺序约束的序列(比如时间序列)的数据类型,前后相邻的数据关联程度很高,在数据分割时不能打乱顺序随机采样,即不能破坏序列的连续性。
代码
sklearn中提供了TimeSeriesSplit函数用于分割这种类型的数据,其主要参数如下:
TimeSeriesSplit():
n_splits:int型,控制产生(训练集+验证集)的数量;
max_train_size:控制最大的时序数据长度;
案例代码:
import numpy as np
X = np.random.randint(1,10,20)
kf = TimeSeriesSplit(n_splits=4)
for train,test in kf.split(X):
print(train,'\n',test)
调参
常用的方法包括网格法,利用一定的步长在参数的值域范围内探索参数最优解,在开始的时候可以选择较大的步长,然后逐步缩小步长逼近最优解。
将数据集划分为三个部分:训练集、验证集、测试集。将训练集数据用于模型训练,验证集(开发集)数据用于模型调参,测试集数据用于验证模型泛化性。
给定包含个样本的数据集,在模型评估与选择过程中由于需要留出一部分数据进行评估测试,事实上我们只使用了一部分数据训练、模型.因此,在模型选择完成后,学习算法和参数配置己选定,此时应该用数据集重新训练模型。这个模型在训练过程中使用了所有个样本,这才是我们最终提交给用户的模型。
性能度量
使用不同的性能度量往往会导致不同的评判结果;这意味着模型的"好坏"是相对的,什么样的模型是好的,不仅取决于算法和数据,还决定于任务需求。
均方误差mean squared error MSE
回归任务常用。学习器预测结果\(f(x)\),真实值\(y\)。
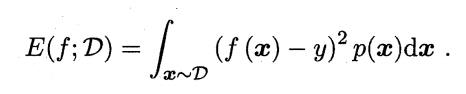
错误率error rate和精度accuracy
错误率:分类错误的样本数站样本总数的比例;
精度:分类正确的样本数站样本总数的比例。
查准率(准确率precision)、查全率(召回率recall)、F1、宏查准率(macro-P)、宏查全率(macro-R)、宏F1(macro-F1)、微查准率(micro-P)、微查全率(micro-R)、微F1(micro-F1)
对于一个二分类问题:
查准率:预测正例中有多少是真实正例;
查全率:真实正例中有多少被预测为正例。
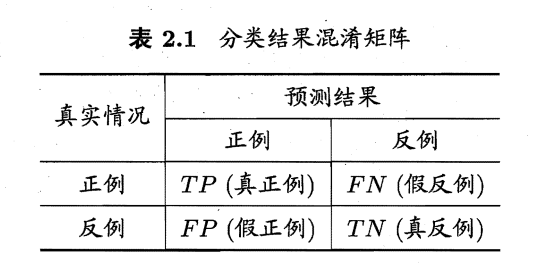
查准率P和查全率R计算公式:
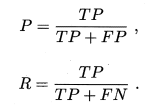
一般来说,查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低。
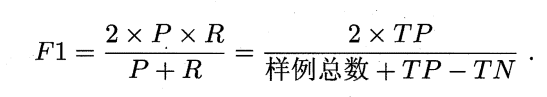
在一些场景中,查准率和查全率的重视程度不同,可以用加权F1——\(F_\beta\)来表达对P和R的不同偏好。
尽可能推荐准确的内容给用户:P重要;尽可能少漏掉逃犯:R重要。
其中\(\beta>0\),其度量了查全率对查准率的相对重要性,\(\beta=1\)退化为标准的F1;\(\beta>1\)时查全率有更大影响;\(\beta<1\)时查准率有更大影响。
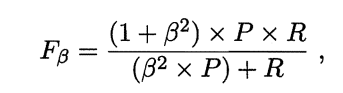
先在各混淆矩阵上分别计算P和R,再计算平均值,得到宏查准率、宏查全率、宏F1:
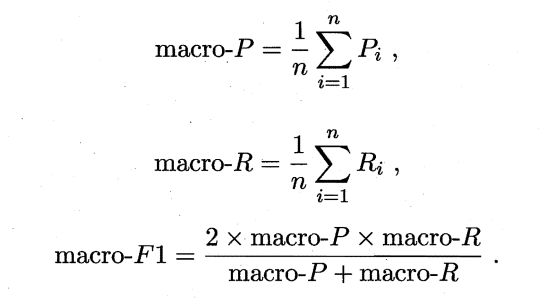
若将混淆矩阵各对应元素先求平均,再基于平均TP、平均FP、平均TN、平均FN可计算微查准率、微查全率、微F1:

