西瓜书阅读笔记——第3章-多分类学习和类别不平衡问题（3.5、3.6）

只记录和补充一些比较容易混淆、易忘、容易表述错误的内容。

多分类学习

考虑N个类别多分类学习的基本思路是“拆解法”，即将多分类任务拆为若干个二分类任务求解。

拆分策略：

一对一 One vs. One OvO

将N个类别两两配对，产生\(N(N-1)/2\)个二分类任务，新样本同时输入所有分类器，得到\(N(N-1)/2\)个分类结果，最终结果可通过投票法产生。
一对其余 One vs. Rest OvR

每次将一个类的样例作为正例，其他所有类的样例作为反例训练分类器，产生\(N\)个二分类任务。新样本输入所有分类器，若仅有一个分类器预测为正类，则对应类别标记为最终分类结果；若多个分类器预测为正类，通常考虑各个分类器的预测置信度，选置信度最大的类别标记作为分类结果。

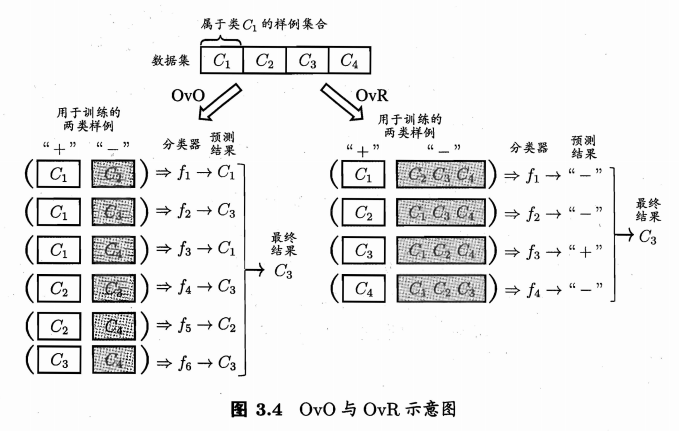
因为OvO要训练更多的分类器，因此其存储开销和测试时间开销通常比OvR更大。但在训练时，OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvR更小。模型的预测性能则取决于具体的数据分布，在多数情形下两者差不多。
多对多 Many vs. Many MvM

每次将若干个类作为正类，其他若干类作为反类。常用的策略如：”纠错输出码“(Error Correcting Output Codes,ECOC)。

类别不平衡问题

类别不平衡(class-imbalance)就是指分类任务中不同类别的训练样例数目差别很大的情况。例如有998个反例，但正例只有个，那么学习方法只需返回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度;然而这样的学习器往往没有价值，因为它不能预测出任何正例。

几率\(\frac{y}{1-y}\)反映了正例可能性与反例可能性之比值，阔值设置为0.5 恰表明分类器认为真实正、反例可能性相同，即分类器决策规则为：

若\(\frac{y}{1-y}>1\) 则预测为正例。

然而当训练集中正例数目(\(m^+\))、反例数目(\(m^-\))不同时，观测几率是\(\frac{m^+}{m^-}\)。由于通常假设训练集是真实样本总体的无偏采样，因此观测几率就代表了真实几率。但事实上这一假设往往不成立，也就是未必能有效地基于训练集观测几率来推断出真实几率，为此有以下三类解决策略：

解决策略

欠采样

直接对训练集里的反类样例进行"欠采样"(undersampling)，即去除一些反倒使得正、反例数日接近然后再进行学习。

优点

欠采样法的时间开销通常远小于过采样法，因为前者丢弃了很多反例，使得分类器训练集远小子初始训练集。

缺点

欠采样法若随机丢弃反例，可能丢失一些重要信息。其代表性算法EasyEnsemble 利用集成学习机制，将反例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样，但在全局来看却不会丢失重要信息。

过采样

对训练集里的正类样例进行"过采样"(oversampling)，即增加一些正例使得正、反例数目接近，然后再进行学习。

缺点

过采样法增加了很多正例，其训练集大于初始训练集。过采样法不能简单地对初始正例样本进行重复来样，否则会招致严重的过拟合，可以通过对训练集的正例进行插值(SMOTE)。

阈值移动threshold-moving

直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，将\(\frac{y'}{1-y'}=\frac{y}{1-y}×\frac{m^-}{m^+}>1\)嵌入到其决策过程中。

只要分类器的预测几率高于观测几率\(\frac{y}{1-y}>\frac{m^+}{m^-}\)则应判定为正例。将右侧移到左侧可转化为：\(\frac{y'}{1-y'}=\frac{y}{1-y}×\frac{m^-}{m^+}>1\)，利用该式对预测值进行调整，称为”再缩放“(rescaling)。

"再缩放"也是"代价敏感学习"(cost-sensitive learning)的基础。在代价敏感学习中将式中的\(m^-\)/\(m^+\)用\(cost^+\)/\(cost^-\)代替即可，其中\(cost^+\)是将正例误分为反例的代价\(cost^-\)是将反例误分为正例的代价。