西瓜书阅读笔记——第6章-支持向量机(核函数6.3、6.6)

引言

在现实任务中，原始样本空间内许并不存在一个能正确划分两类样本的超平面。

将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

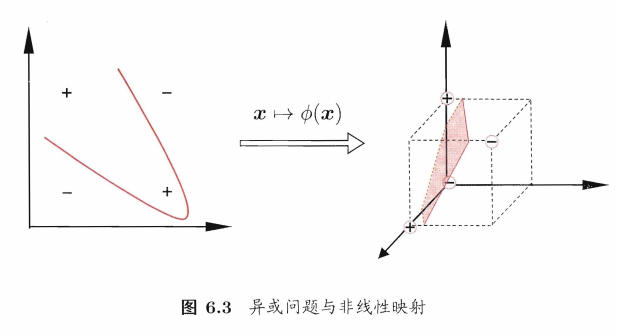
令\(\phi(\mathbf x)\)表示将\(\mathbf x\)映射后的特征向量。那么，在特征空间中划分超平面所对应的模型可表示为： \[ f(\mathbf x)=\mathbf w^T\phi(\mathbf x)+b \] 则其策略为： \[ \begin{align} \min_{\mathbf w,b}& \frac{1}{2}||\mathbf w||^2 \\s.t. 1-y_i(\mathbf w^T&\phi(\mathbf x_i)+b)≤0, i=1,2,...,m \end{align} \] 其对偶问题为： \[ \begin{align} \max_{\mathbf α} \sum_{i=1}^mα_i-\frac{1}{2}\sum_{i=1}^m&\sum_{j=1}^mα_iα_jy_iy_j\phi(\mathbf x_i)^T\phi(\mathbf x_j) \\s.t. &\sum_{i=1}^mα_iy_i, \\ α_i≥0, &i=1,2,...,m \end{align} \] 可以看到上述涉及计算\(\phi(\mathbf x_i)^T\phi(\mathbf x_j)\)，也就是需要计算样本\(\mathbf x_i,\mathbf x_j\)映射到特征空间之后的内积。由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算该值通常是困难的。

核函数kernel function

设想这样一个函数： \[ \kappa(\mathbf x_i,\mathbf x_j)=<\phi(\mathbf x_i),\phi(\mathbf x_j)>=\phi(\mathbf x_i)^T\phi(\mathbf x_j) \] 样本\(\mathbf x_i,\mathbf x_j\)在特征空间的内积等于它们在原始样本空间中通过函数\(κ(·,·)\)计算的结果。\(κ(·,·)\)称为核函数。

可得到： \[ \begin{align} f(\mathbf x)&=\mathbf w^T\phi(\mathbf x)+b \\&=\sum_{i=1}^mα_iy_i\phi(\mathbf x_i)^T\phi(\mathbf x_j)+b \\&=\sum_{i=1}^mα_iy_i\kappa(\mathbf x_i,\mathbf x_j)+b \end{align} \] 此显示出模型最优解可通过训练样本的核函数展开，这一展式亦称"支持向量展式"(support vector expansion)。