西瓜书阅读笔记——第6章-支持向量机(软间隔6.4、6.5)
西瓜书阅读笔记——第6章-支持向量机(软间隔6.4、6.5)
强烈推荐配合西瓜书阅读使用的南瓜书和南瓜书作者录制的学习视频【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集。
上一篇博客讨论线性可分的数据集,但事实上在现实任务中,线性不可分的情形才是最常见的,因此需要允许支持向量机犯错,因此引入软间隔的概念。
软间隔支持向量机
软间隔soft margin
硬间隔hard margin:所有样本均满足约束,即所有样本都必须划分正确。
软间隔soft margin:允许部分样本不满足约束。


据此可设计优化目标为:


其他常见的替代损失(surrogate loss)函数包括:
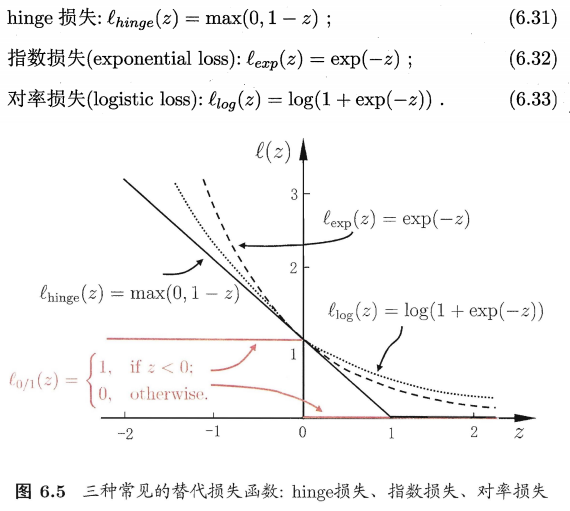
进一步,引入"松弛变量"(slack variables)\(\xi_i≥0\),表示每个样本不满足约束\(y_i(\mathbf w^T\mathbf x_i+b)≥1\)的程度。

同样可证明该问题为凸优化问题,(见西瓜书阅读笔记——第6章-支持向量机(硬间隔6.1、6.2) | 冬于的博客 (ifwind.github.io));
因此也可采用硬间隔支持向量机相同的求解方式求解。

与硬间隔支持向量机的拉格朗日对偶问题进行对比:

两者唯一的差别就在于对偶变量的约束不同。
采用与硬间隔支持向量机相同的方法进行求解,满足一下KKT条件:

求解主问题转化为先对拉格朗日函数求\(\mathbf x\)的偏导令其为0,带到拉格朗日对偶函数中求解出\(\mathbf μ,\mathbf α\),再带回求解\(\mathbf w,b\)得到超平面的解。
形如支持向量机损失函数的更一般的形式
优化目标中的第一项用来描述划分超平面的"间隔"大小,另一项\(\sum_{i=1}^m\ell (f(\mathbf x_i),y_i)\)用来表述训练集上的误差,可写为: \[ \min_f\space \Omega(f)+C\sum_{i=1}^m\ell (f(\mathbf x_i),y_i) \]
结构风险(structural risk) \(\Omega(f)\)
用于描述模型的某些性质。从经验风险最小化的角度来看\(\Omega(f)\)表述了我们希望获得具有何种性质的模型(例如希望获得复杂度较的模型), 这为引入领域知识和用户意图提供了途径;另一方面,该信息助于削减假设空间从而降低了最小化训练误差的过拟合风险。从这个角度,其也可称为正则化(regularization)项,上式称为正则化问题,\(C\)称为正则化常数。
经验风险(empirical risk) \(\sum_{i=1}^m\ell (f(\mathbf x_i),y_i)\)
用于描述模型与训练数据的契合程度。
惩罚系数\(C\)
用于对二者进行折中。
支持向量回归SVR
事实上,支持向量回归和支持向量机不是一回事,只是为了贴近SVM损失函数的形式设计了损失函数。


与支持向量机类似,可利用拉格朗日对偶求解:
引入拉格朗日乘子(\(\mathbf α,\mathbf {\hat{α}},\mathbf μ,\mathbf {\hat{μ}}\)),得到拉格朗日函数:
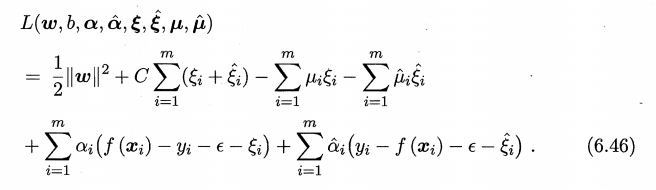
对除了拉格朗日乘子以外的参数(\(\mathbf w,b, \xi_i,\hat\xi\))求一阶偏导,并令一阶偏导为0:

得到SVR对偶问题:

上述过程满足的KKT条件有:

最后求得SVR的解为:

参考文献
【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
*视频的PPT:https://pan.baidu.com/s/1g1IrzdMHqu6XyG0bFIcFsA 提取码: 7nmd
