西瓜书阅读笔记——第9章-聚类
西瓜书阅读笔记——第9章-聚类
什么是聚类
无监督学习,通过对无标记对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。
两个基本问题:
- 性能度量;
- 距离计算。
聚类性能度量
有效性指标,评估聚类结果的好坏,可以作为聚类过程的优化目标,以达到符合要求的聚类结果。
希望聚类结果的:"簇内相似度"(intra-cluster similarity)高,且"簇间相似度"(inter-cluster similarity)低。
根据是否有参考模型,可以将聚类性能度量分为两类:
- 外部指标external index:将聚类结果与某个"参考模型"(reference model)进行比较;
- 内部指标internal index:直接考察聚类结果而不利用任何参考模型。
外部指标external index
聚类划分的簇划分集合\(C={C_1,C_2...C_k}\),参考模型的簇划分集合\(C^*={C^*_1,C^*_2...C^*_s}\),一个样本属于\(C_i\)且属于\(C^*_i\)。
对于训练集中任意两个样本,簇划分有四种情况:
- 两个样本在\(C\)中同一个簇,且在\(C^*\)中同一个簇,样本对数量为\(a\);
- 两个样本在\(C\)中同一个簇,且在\(C^*\)中不同簇,样本对数量为\(b\);
- 两个样本在\(C\)中不同簇,且在\(C^*\)中同一个簇,样本对数量为\(c\);
- 两个样本在\(C\)中不同簇,且在\(C^*\)中不同簇,样本对数量为\(d\);
如果有\(m\)个样本,则有:\(a+b+c+d=\frac{m(m-1)}{2}\)
据此导出以下常用度量聚类性能的外部指标:
Jaccard系数(Jaccard Coefficient,简称JC)
值在[0,1]区间,值越大越好。 \[ JC=\frac{a}{a+b+c} \]
FM指数(Fowlkes and Mallows lndex,简称FMI)
值在[0,1]区间,值越大越好。 \[ FMI=\sqrt{\frac {a}{a+b}·\frac {a}{a+c}} \]
Rand指数(Rand Index,简称RI)
值在[0,1]区间,值越大越好。 \[ RI=\frac{a+d}{a+b+c+d}=\frac{2(a+d)}{m(m-1)} \]
内部指标internal index
距离计算
距离度量需满足的基本性质:
- 非负性:\(dist(\mathbf x_i,\mathbf x_j)≥0\);
- 同一性:\(dist(\mathbf x_i,\mathbf x_j)=0当且仅当\mathbf x_i=\mathbf x_j\);
- 对称性:\(dist(\mathbf x_i,\mathbf x_j)=dist(\mathbf x_j,\mathbf x_i)\);
- 直递性:\(dist(\mathbf x_i,\mathbf x_j)≤dist(\mathbf x_i,\mathbf x_k)+dist(\mathbf x_k,\mathbf x_j)\)。
用于有序属性的距离度量:闵可夫斯基距离
\[ dist_{mk}(\mathbf x_i,\mathbf x_j)=(\sum_{u=1}^n|x_{iu}-x_{ju}|^p)^{\frac {1}{p}} \]
当\(p≥1\),上式显然满足距离度量基本性质。
当\(p=1\),闵可夫斯基距离为曼哈顿距离。
当\(p=2\),闵可夫斯基距离为欧氏距离。
用于无序属性的距离度量:VDM(Value Difference Metric)
\(m_{u,a}\)表示在属性\(u\)上取值为\(a\)的样本数,\(m_{u,a,i}\)表示在第\(i\)个样本簇中在属性\(u\)上取值为\(a\)的样本数,\(k\)为样本簇数,则属性\(u\)上两个离散值\(a\)和\(b\)之间的VDM距离为: \[ VDM_p(a,b)=\sum_{i=1}^{k}|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|^p \]
混合属性距离度量:MinkovDM
假定有\(n_c\)个有序属性\(n-n_c\)个无序属性,令有序属性排列在无序属性之前,则: \[ MinkovDM_p(\mathbf x_i,\mathbf x_j)=\big((\sum_{u=1}^{n_c}|x_{iu}-x_{ju}|^p)+\sum_{u={n_c}+1}^{n}VDM_p(x_{iu},x_{ju})\big)^{\frac {1}{p}} \]
加权距离度量
以加权闵可夫斯基距离为例: \[ disy_{wmk}(\mathbf x_i,\mathbf x_j)=(\sum_{u=1}^{n}w_u·|x_{iu}-x_{ju}|)^{\frac{1}{p}} \] 其中\(w_u≥0,\sum_{u=1}^{n}w_u=1\)。
其他
基于某种形式的距离定义“相似度度量”,距离越大,相似度越小,但相似度度量未必一定满足距离度量的所有基本性质。若距离不再满足直递性,这样的距离称为"非度量距离"(nonmetric distnce)。
在不少现实任务中,有必要基于数据样本来确定 合适的距离计算式,这可通过距离度量学习(distance metric learning)来实现。
聚类方法分类
原型聚类
基于原型的聚类,假设聚类结构能通过一组原型刻画。算法先对原型进行初始化,然后对原型进行迭代更新求解。
k-means算法
针对聚类所得簇划分求最小平方误差: \[ E=\sum_{i=1}^k\sum_{x \in C_i}||\mathbf x-\mathbf \mu_i||^2_2 \] 其中\(\mathbf \mu_i=\frac{1}{|C_i|}\sum_{x \in C_i}\mathbf x\)是簇\(C_i\)的均值向量,上式直观来看在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度。
最小化上式是一个NP难题,k-means算法采用贪心策略,通过迭代优化近似求解。
算法流程如下图所示:

学习向量量化Learning Vector Quantization LVQ
LVQ的目标也是学得一组\(n\)维原型向量\({\mathbf p_1,\mathbf p_2,...,\mathbf p_q}\),每个原型向量代表一个聚类簇。因此,可实现对样本空间的簇划分。对任意样本\(\mathbf x\),它将被划入与其距离最近的原型向量所代表的簇中;换言之,每个原型向量\(\mathbf p_i\)定义了与之相关的一个区域\(R_i\),该区域中每个样本与\(\mathbf p_i\)的距离不大于它与其他原型向量\(\mathbf p_{i'}(i'≠i)\)的距离。若将\(R_i\)中样本会用原型向量表示,则可实现数据的"有损压缩"(Iossy compression),这称为"向量量化"(vector quantization)。LVQ由此而得名。
特别的是,LVQ的学习过程利用了样本类别标记的监督信息来辅助聚类。
LVQ算法流程如下图所示,关键在于6-10行,直观上,若样本\(\mathbf x_j\)最近的原型向量\(\mathbf p_{i^*}\)与其标记相同,则让原型向量\(\mathbf p_{i^*}\)不断向\(\mathbf x_j\)靠拢,否则不断远离:

高斯混合聚类
高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型。高斯分布完全由均值向量\(\mu\)和协方差矩阵\(\Sigma\)这两个参数确定。
可定义高斯混合分布为: \[ p_\mathcal M(\mathbf x)=\sum_{i=1}^k\alpha_i·p(\mathbf x|\mathbf{\mu_i}, \mathbf \Sigma_i) \] \(\mathbf x\)服从高斯分布,其概率密度函数为\(p(\mathbf x|\mathbf{\mu_i}, \mathbf \Sigma_i)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^\frac{1}{2}}e^{\frac{1}{2}(\mathbf x-\mathbf {\mu})^T\Sigma^{-1}(\mathbf x-\mathbf {\mu})}\)。
该分布共由\(k\)个混合成分组成,每个混合成分对应一个高斯分布,其中\(\mathbf {\mu_i}\)与\(\mathbf \Sigma_i\)是第\(i\)个高斯混合成分的参数,而\(\alpha_i>0,\sum_{i=1}^k\alpha_i=1\),是相应的“混合系数”(mixture coefficient)。
模型的参数\(\{(\alpha_i,\mathbf{\mu_i}, \mathbf \Sigma_i)|1≤i≤k\}\)可以采用极大似然估计,然后最大化(对数)似然,采用EM算法进行迭代优化求解。
高斯混合聚类算法流程如下:

密度聚类
"基于密度的聚类"(density-based clustering),此类算法假设聚类结构能通过样本分布的紧密程度确定。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
基于一组“领域”参数\((\epsilon,MinPts)\)来刻画样本分布的紧密程度。
DBSCAN算法有以下概念:

先根据给定的邻域参数\((\epsilon,MinPts)\)从数据集中找出所有核心对象为“种子”,再以任一核心对象出发,找出其密度可达的样本确定相应的聚类簇,直到所有核心对象被访问过为止。
DBSCAN算法流程图如下图所示:

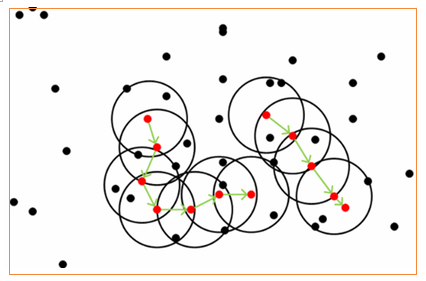
在上图中,第一步就是寻找红色的核心点,第二步就是用绿色箭头联通红色点。图中点以绿色线条为中心被分成了两类。没在黑色圆中的点是噪声点。
层次聚类
层次聚类(harchical clustering)在不同层次对数据集进行分,从而形成树形的聚类结构。数据集的划分可采用"自底向上"的聚合策略,也可采"自顶向下"的分拆策略。
- 凝聚:自底向上。首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有的对象都在一个簇中,或者某个终结条件被满足。
- 分裂:自顶向下。首先将所有对象置于同一个簇中,然后逐渐细分为越来越小的簇,直到每个对象自成一簇,或者达到了某个终止条件。(较少用)
自底向上的AGNES(AGglomerative NESting)
先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直到达到预设的聚类簇个数。
显然关键是如何计算聚类簇之间的距离。每个簇是一个样本集合,只需要用关于集合的某种距离度量即可。
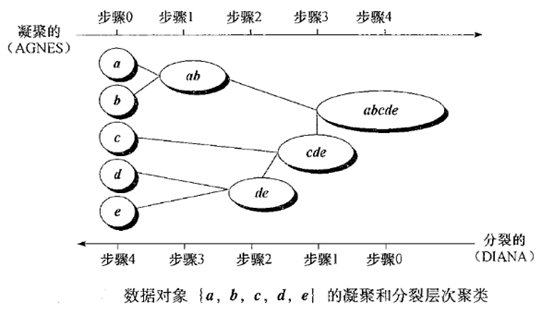
算法流程如下:

根据所选择度量距离的方法不同,AGNES算法也被相应称作:\(d_{min}\)单链接、\(d_{max}\)全链接、\(d_{avg}\)均链接算法。
聚类python实战
sklearn包中的K-Means算法
函数:
sklearn.cluster.KMeans主要参数:
n_clusters:要进行的分类的个数,即上文中k值,默认是8
max_iter :最大迭代次数。默认300
min_iter :最小迭代次数,默认10
init:有三个可选项
'k-means ++':使用k-means++算法,默认选项
'random':从初始质心数据中随机选择k个观察值
第三个是数组形式的参数
n_jobs: 设置并行量 (-1表示使用所有CPU)主要属性:
cluster_centers_ :集群中心的坐标
labels_ : 每个点的标签
官网示例:
from sklearn.cluster import KMeans |
sklearn包中的Hierarchical Clustering
函数
sklearn.cluster.AgglomerativeClustering主要参数(详细参数)
n_clusters:聚类的个数
linkage:指定层次聚类判断相似度的方法,有以下三种:
ward:组间距离等于两类对象之间的最小距离。(即single-linkage聚类)
average:组间距离等于两组对象之间的平均距离。(average-linkage聚类)
complete:组间距离等于两组对象之间的最大距离。(complete-linkage聚类)主要属性
labels_: 每个数据的分类标签
算法示例:
from sklearn.datasets.samples_generator import make_blobs |
sklearn包中的DBSCAN
函数
sklearn.cluster.DBSCAN主要参数(详细参数)
eps:两个样本之间的最大距离,即扫描半径
min_samples :作为核心点的话邻域(即以其为圆心,eps为半径的圆,含圆上的点)中的最小样本数(包括点本身)。主要属性
core_sample_indices_:核心样本指数。(此参数在代码中有详细的解释)
labels_:数据集中每个点的集合标签给,噪声点标签为-1。
算法示例
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle ##python自带的迭代器模块
from sklearn.preprocessing import StandardScaler
##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=750
##生产数据:此实验结果受cluster_std的影响,或者说受eps 和cluster_std差值影响
X, lables_true = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.4,
random_state =0)
##设置分层聚类函数
db = DBSCAN(eps=0.3, min_samples=10)
##训练数据
db.fit(X)
##初始化一个全是False的bool类型的数组
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
'''
这里是关键点(针对这行代码:xy = X[class_member_mask & ~core_samples_mask]):
db.core_sample_indices_ 表示的是某个点在寻找核心点集合的过程中暂时被标为噪声点的点(即周围点
小于min_samples),并不是最终的噪声点。在对核心点进行联通的过程中,这部分点会被进行重新归类(即标签
并不会是表示噪声点的-1),也可也这样理解,这些点不适合做核心点,但是会被包含在某个核心点的范围之内
'''
core_samples_mask[db.core_sample_indices_] = True
##每个数据的分类
lables = db.labels_
##分类个数:lables中包含-1,表示噪声点
n_clusters_ =len(np.unique(lables)) - (1 if -1 in lables else 0)
##绘图
unique_labels = set(lables)
'''
1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
2)plt.cm 一个颜色映射模块
3)生成的每个colors包含4个值,分别是rgba
4)其实这行代码的意思就是生成4个可以和光谱对应的颜色值
'''
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
plt.figure(1)
plt.clf()
for k, col in zip(unique_labels, colors):
##-1表示噪声点,这里的k表示黑色
if k == -1:
col = 'k'
##生成一个True、False数组,lables == k 的设置成True
class_member_mask = (lables == k)
##两个数组做&运算,找出即是核心点又等于分类k的值 markeredgecolor='k',
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=14)
'''
1)~优先级最高,按位对core_samples_mask 求反,求出的是噪音点的位置
2)& 于运算之后,求出虽然刚开始是噪音点的位置,但是重新归类却属于k的点
3)对核心分类之后进行的扩展
'''
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()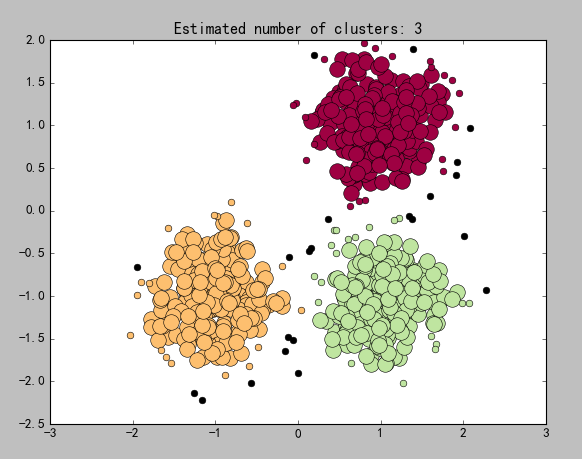
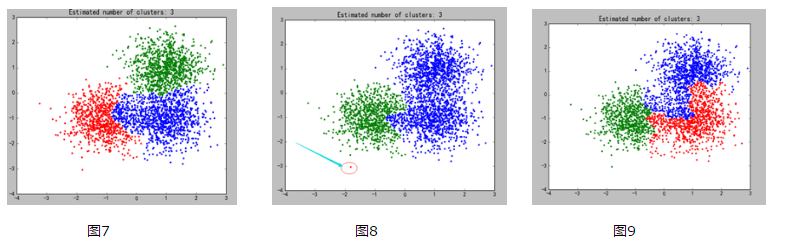
如果不进行第二步中的扩展,所有的小圆点都应该是噪声点(不符合第一步核心点的要求)
算法优缺点
a)优点
可以发现任意形状的聚类
b)缺点
随着数据量的增加,对I/O、内存的要求也随之增加。
如果密度分布不均匀,聚类效果较差
sklearn包中的GaussianMixtureModel
函数`from sklearn.mixture.GaussianMixture
主要参数(详细参数)
n_components :高斯模型的个数,即聚类的目标个数
covariance_type : 通过EM算法估算参数时使用的协方差类型,默认是"full"
full:每个模型使用自己的一般协方差矩阵
tied:所用模型共享一个一般协方差矩阵
diag:每个模型使用自己的对角线协方差矩阵
spherical:每个模型使用自己的单一方差算法示例:代码中有详细讲解内容
import matplotlib.pyplot as plt |