西瓜书阅读笔记——第5章-神经网络
西瓜书阅读笔记——第5章-神经网络
M-P神经元模型
神经元接收到来自n个其他神经元传递过来的"输入信号"{\(x_1,x_2,...,x_n\)},输入信号通过带权重{\(w_1,w_2,...,w_n\)}进行加权和,神经元接收到的总输入值减去神经元的"阈值"\(\theta\),然后通过"激活函数"(activation function)\(f(·)\)处理以产生神经元输出\(y\)。
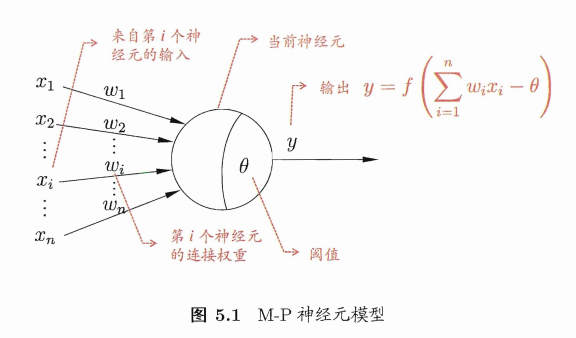
单个M‑P神经元:感知机( 阶跃函数sgn作激活函数)、对数几率回归(sigmoid作激活函数) 多个M‑P神经元:神经网络。
感知机 Perceptron
模型
数学表示
感知机(Perceptron)由两层神经元组成。输入层接收外界输入信号后传递给输出层,输出层是M-P神经元,亦称"阈值逻辑单元"(threshold logic unit)。
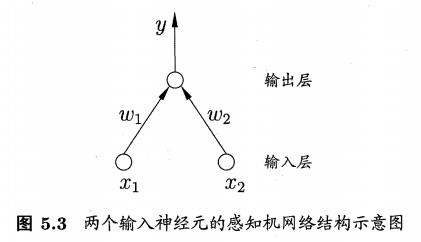
感知机只能实现逻辑与、或、非运算。
激活函数为sgn (阶跃函数)的神经元: \[ \begin{align} y = sgn(\mathbf w^T\mathbf x−θ)= \left\{ \begin{array}{ll} 1, & \mathbf w^T\mathbf x−θ ≥0\\ 0, & \mathbf w^T\mathbf x−θ <0 \end{array} \right. \end{align} \] 其中, \(x∈\mathbb R^n\)为样本的特征向量,是感知机模型的输入,\(\mathbf w,\theta\)是感知机模型的参数,\(\mathbf w\)为权重, \(\theta\)为阈值。
几何理解
从几何角度来说,给定一个线性可分的数据集\(T\),感知机的学习目标是求得能对数据集\(T\)中的正负样本完全正确划分的超平面,其中\(\mathbf w^T\mathbf x−θ\)即为超平面方程。
感知机(单层)只能解决线性可分的数据集。
什么是线性可分的数据集?
什么是超平面?
N维线性空间的超平面的维度为N-1,且一定经过原点。可以把线性空间分成不相交的两部分。
比如:
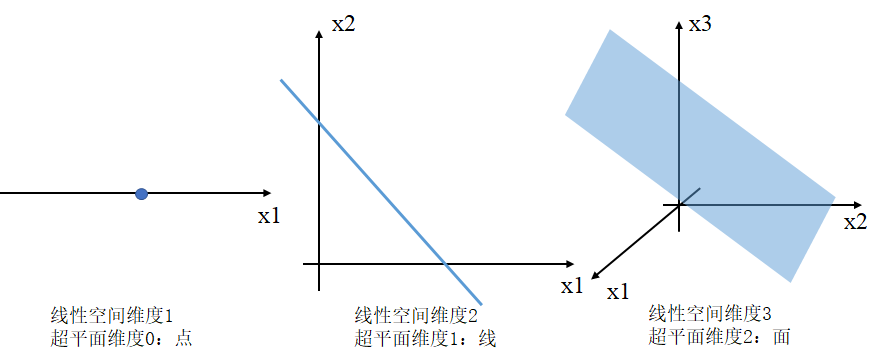
n维空间的超平面\(\mathbf w^T\mathbf x−θ=0,\mathbf w,\mathbf x\in \mathbb R^n\)有以下性质:
超平面方程不唯一
当\(\mathbf w^T\mathbf x−θ=0\)左右两边同乘以一个常数λ,方程改变,但仍为数据集超平面;
此外,如下图所示,黄色线和蓝色线都可以将正负例区分开。
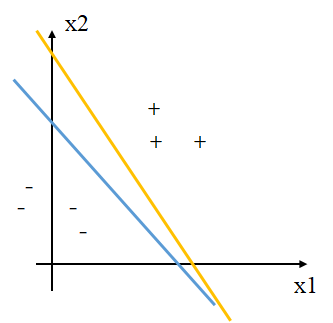
法向量\(\mathbf w\)垂直于超平面
蓝色线为超平面\(x_1+x_2-1=0\),黄色向量为该超平面的\(\mathbf w\)。
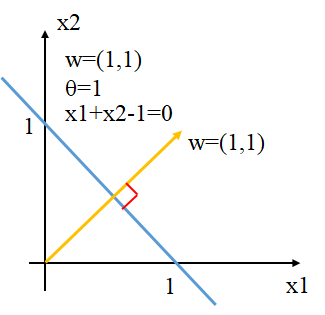
法向量\(\mathbf w\)和位移项\(\theta\)确定一个唯一超平面
\(\mathbf w\)决定超平面的转向,\(\theta\)决定超平面距离原点的距离。
法向量\(\mathbf w\)指向的那一半空间为正空间,另一半为负空间。
策略
给定训练集\(T\),权重\(\mathbf w =\{w_1,w_2,...,w_n\}\)以及阈值\(\theta\)可以通过学习得到。首先将随机初始化\(\mathbf w,b\),将全体训练样本\(T\)代入模型找出误分类样本,假设此时误分类样本集合为\(M\subseteq T\),对任意一个误分类样本\((\mathbf x,y)\in M\)来说,当\(\mathbf w^T\mathbf x−θ≥0\)时,模型输出值为\(\hat y=1\),样本真实标记\(y=0\) ;反之,当\(\mathbf w^T\mathbf x−θ<0\)时,模型输出值为\(\hat y=0\),样本真实标记为\(y=1\)。
那么以下的公式在上两种情形中恒成立: \[ (\hat y-y)(\mathbf w^T\mathbf x−θ)≥0 \] 进一步,对于数据集\(T\),可以定义损失函数为: \[ L(\mathbf w, θ)=\sum_{x\in M}(\hat y-y)(\mathbf w^T\mathbf x−θ) \] 显然此损失函数是非负的。如果没有误分类点,损失函数值是 \(0\)。而且,误分类点越少,误分类点离超平面越近,损失函数值就越小。因此,给定数据集\(T\),损失函数 \(L(\mathbf w, θ)\) 是关于\(\mathbf w, θ\)的连续可导函数。
算法
\(η\in(0,1)\)为学习率控制着算法每一轮迭代中的更新步长,若太大则容易振荡,太小则收敛速度又会过慢,常设置为\(η=0.1\)。
损失函数的全局最小值是唯一的,但使得损失函数达到最小的\(\mathbf w\)(此时的\(\mathbf w\)已经包括了阈值\(\theta\))不唯一,参照前面超平面不唯一的解释。
神经网络
前面提到,感知机(单层功能神经元)只能分类线性可分的数据集,要解决非线性可分问题,可以用多层功能神经元。
多层前馈神经网络multi-layer feedforward neural networks
模型
每层神经元与下一层神经元全部互相连接(全连接),神经元之间不存在同层连接,也不存在跨层连接。”前馈“指的是网络拓扑结构上不存在环或回路,而不是信号不能反向传播。
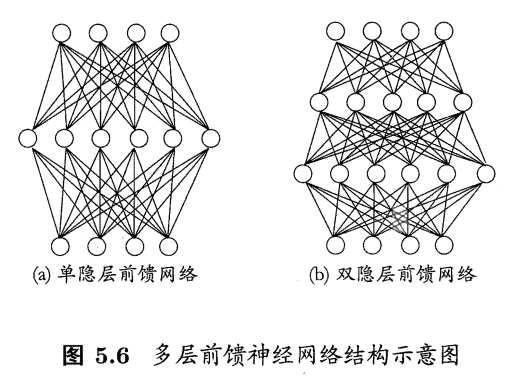
因为输入层神经元仅仅接受输入,而不进行函数处理,隐层与输出层才包含功能神经元,因此下图(a)称为”单隐层网络“。只要包含隐藏层即可称为多层网络。
通用近似定理
只需一个包含足够多神经元的隐层,多层前馈网络(最经典的神经网络之一)就能以任意精度逼近任意复杂度的连续函数。
策略

算法
反向传播(误差逆传播error BackPropagation,BP)
BP是一个迭代学习算法,在迭代的每一轮中对任意参数\(v\)采用以下更新估计式: \[ v\leftarrow v+\nabla v \]
算法流程

标准BP算法演算示例
假设现在有一个单隐层网络(下图),其隐藏层中的激活函数全为sigmoid函数,且当前要完成的任务为一个(多输出)回归任务,因此损失函数可以采用均方误差。
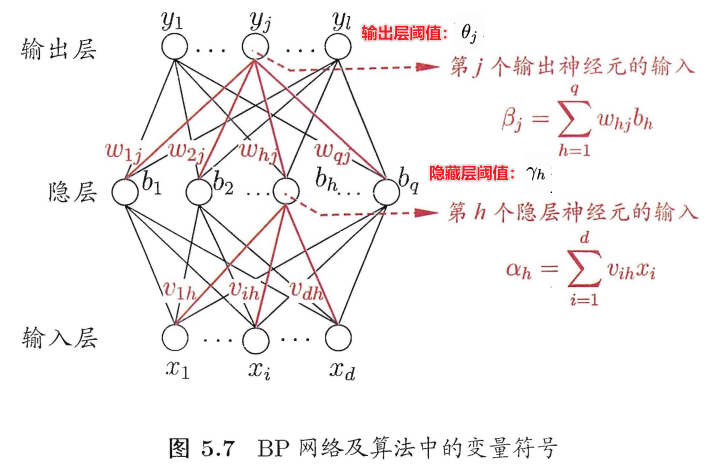
对于某个训练样本\((\mathbf x_k,\mathbf y_k)\),其中\(\mathbf y_k=(y_1^k,y_2^k,...,y_l^k)\),则假设该网络输出为\(\mathbf {\hat y_k}=(\hat y_1^k,\hat y_2^k,...,\hat y_l^k)\),则该样本的均方误差(损失)为: \[ E_k=\frac {1}{2}\sum_{j=1}^l (\hat y _j^k-y_j^k)^2 \] 对以上图中单隐层网络进行标准BP算法的演示:
总共需要求解输入层到隐藏层的连接权重\(\mathbf v\)和阈值\(\mathbf γ\),隐藏层到输出层的连接权重\(\mathbf w\)和阈值\(\mathbf θ\)。
以\(\mathbf v\)中的\(v_{ih}\)为例
\(v_{ih}\)通过影响第\(h\)个隐层神经元的输入值\(α_h\),再影响到其输出值\(b_h\),然后进一步影响到输出层神经元所有的(由于全连接)输入值\(\{β_1,β_2...,β_l\}\),再影响到其输出值\(\{\hat y_1^k,\hat y_2^k...,\hat y_l^k\}\),最后影响到\(E_k\),根据”链式法则“则有:

则:
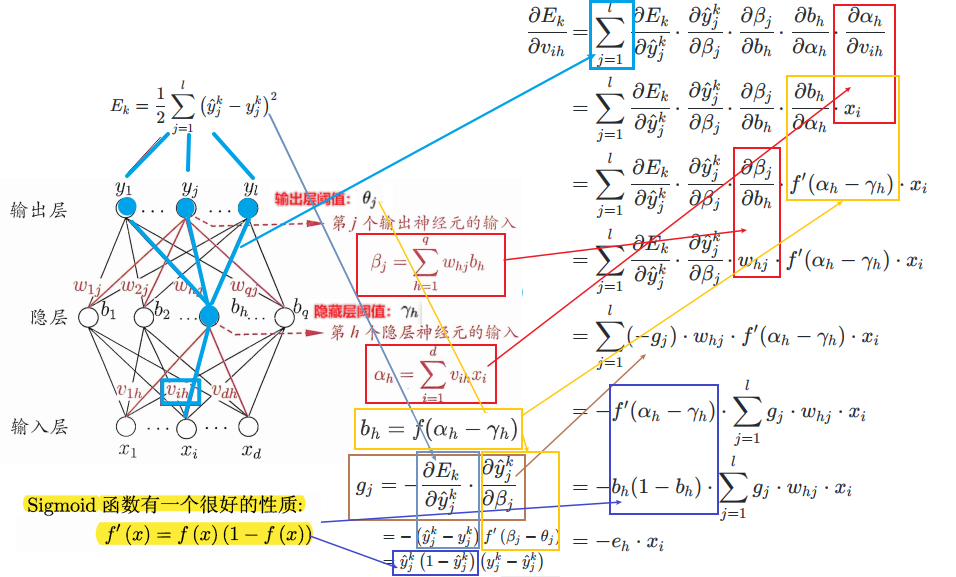
可得:
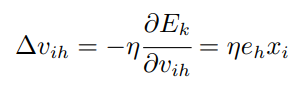
以\(\mathbf θ\)中的\(θ_{j}\)为例

则:

以\(\mathbf γ\)中的\(γ_{h}\)为例
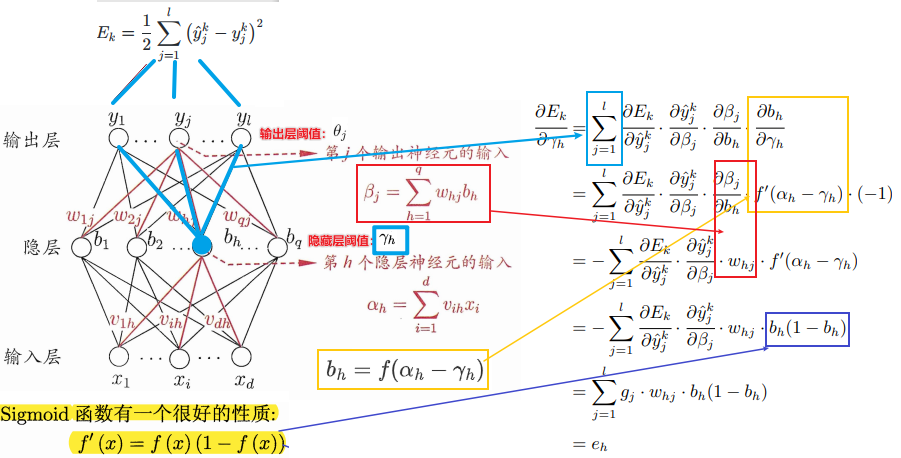
可得:
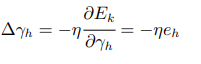
以\(\mathbf w\)中的\(w_{hj}\)为例
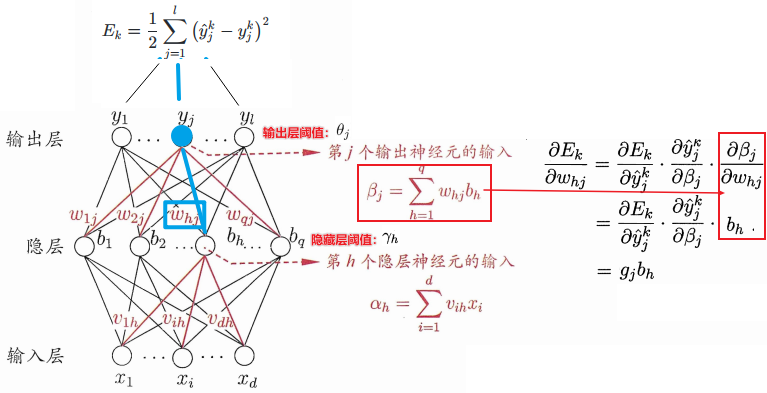
可得:
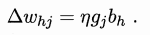
TIPS
有时为了做精细调节,不同层之间的学习率可不同,比如此网络中,可令式(5.11)(5.12)使用\(η_1\),式(5.13)(5.14)使用\(η_2\)。
标准BP算法缺点
- 标准BP算法每次更新只针对单个样例\(E_k\),参数更新得非常频 繁;
- 对不同样例进行更新的效果可能出现"抵消"现象;
- 为了达到同样的累积误差极小点,往往需进行更多次数的迭代。
累积BP算法
累积BP算法最小化训练集\(T\)上的累计误差: \[ E=\frac{1}{m}\sum_{k=1}^mE_k \] 在读取整个训练集一遍后("一轮"(one round/one epoch))才对参数进行更新,其参数更新的频率低得多;但在很多任务中,累积误差下降到一定程度之后,进一步下降会非常缓慢,这时标准BP往往会更快获得较好的解,尤其是在训练集非常大时更明显。
缓解神经网络的过拟合问题
早停(early stopping)
将数据分成训练集和验证集,训练、集用来计算梯度、更新连权和阈值。验证集用来估计误差,若训练集误差降低,但验证集误差升高则停止训练,同时返回具有最小验证集误差的连接权和阈值。
正则化(regularization)
在误差目标函数中增加一个用于描述网络复杂度的部分,
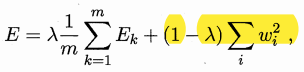
其中\(λ\in(0,1)\)用于对经验误差与网络复杂度这两项进行折中,通常通过交叉验证法来估计。
参数寻优
如何跳出局部最小,进一步接近全局最小?
大多是启发式算法:
多组不同参数初始化多个神经网络
取其中误差最小的解作为最终参数。从不同初始点开始搜索可能陷入不同的局部最小,从中选取更接近全局最小的结果。
模拟退火
在每一步都以一定概率接受比当前解更差的结果,从而有助于”跳出“局部极小(也有可能”跳出“全局最小),每次迭代接受”次优解“的概率随时间/迭代次数逐渐降低。
随机梯度下降
与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素。即便陷入局部极小点,它计算出的梯度仍可能不为零,有机会跳出局部极小继续搜索。
其他几种特别常见的神经网络
RBF(径向基函数,Radial Basis Function)网络
单隐层前馈神经网络,使用径向基函数作为隐层神经元激活函数,输出层是对隐层神经元输出的线性组合。
两步训练RBF网络:
- 确定神经元中心\(\mathbf c_i\)常用的方式包括随机采样、聚类等;
- 利用BP算法等来确定参数\(w_i\)和\(β_i\).
ART(自适应谐振理论,Adaptive Resonance Theory)网络
一种基于竞争型学习(competitive learning)策略的网络。
竞争型学习是神经网络中一种常用的无监督学习策略,在使用该策略时,网络的输出神经元相互竞争,每一时刻仅有一个竞 争获胜的神经元被激活,其他神经元的状态被抑制。亦称"胜者通吃"(winner-take-all)原则。
可进行增量学习(incremental learning)或在线学习(online learning)。
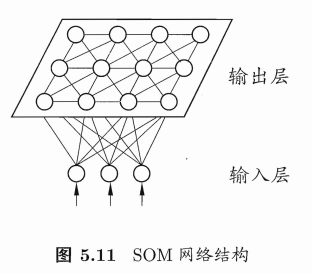
SOM(自组织映射,Self-Organizing Map)网络
一种竞争学习型的无监督神经网络,能将高维输入数据映射到低维空间(通常为二维),同时保持输入数据在高维空间的拓扑结构,即,将高维空间中相似的样本点映射到网络输出层中的邻近神经元。
SOM的训练目标就是为每个输出层神经元找到合适的权向量,以达到保持拓扑结构的目的。
结构自适应网络
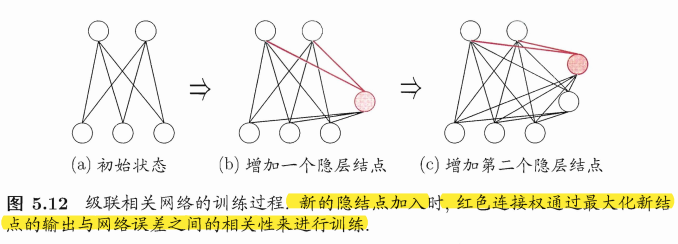
结构自适应网络结构也当作学习的目标之一,并希望能在训练过程中找到最利合数据特点的网络结构。级联相关(Cascade-Correlation是结构自适应网络的一种。
特点
级联相关网络无需设置网络层数、隐层神经元数目,且训练速度较快,但其在数据较小时易过拟合。
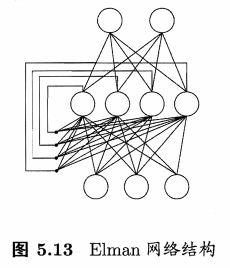
Elman(RNN的一种)
"递归神经网络"(recurrent/recursive neural networks)允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号。网络在时刻的输出状态不仅与时刻\(t\)的输入有关,还与时刻\(t-1\)的网络状态有关,从而能处理与时间有关的动态变化。
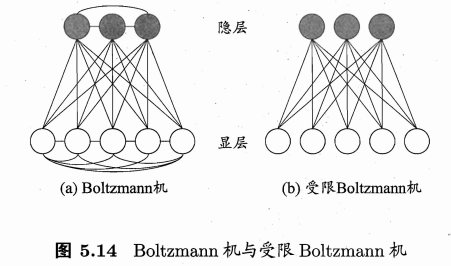
Boltzmann机
Boltzmann机是一种"基于能量的模型"(energy-based model)。为网络状态定义一个"能量"(energy),能量最小化时网络达到理想状态,而网络的训练就是在最小化这个能量函数。
Boltzmann机是全连接的,复杂度很高,现实中常采用仅保留显层与隐层之间的连接。
神经网络存在的问题
面对一个具体场景,神经网络该做多深?多宽?
没有理论支撑,只能依靠实验。
面对一个具体场景,神经网络的结构该如何设计才最合理?
比如对于图像结构的数据CNN表现更好,而序列结构的数据(如文本)RNN更好。
面对一个具体场景,神经网络的输出结果该如何解释?
神经网络的可解释性。
深度学习
本质
特征学习feature learning/表示学习representation learning。
节省训练开销的方法
待求参数量大,数据量小容易过拟合,数据量大训练开销大。
预训练+微调
预训练pre-training:每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,本层隐节点的输出作为下一层隐节点的输入;
微调fine-tuning:在预训练全部完成后,再对整个网络进行”微调“。
可视为将大量参数分组,对每组先找到局部看来比较好的设置,然后再基于这些局部较优的结果联合起来远行全局寻优。在利用了模型大量参数所提供的自由度的同时,有效地节省了训练开销。
权重共享(weight sharing)
卷积神经网络(Convolutional Neural Network,CNN)
包括卷积层、采样层/池化/汇合Pooling等层,每一层的每一组(每个channel)神经元都是相同的连接权重,大幅减少训练参数数目。
参考文献
【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
*视频的PPT:https://pan.baidu.com/s/1g1IrzdMHqu6XyG0bFIcFsA 提取码: 7nmd


